栈的定义:
栈(stack)是限定仅在表尾进行插入和删除的线性表。
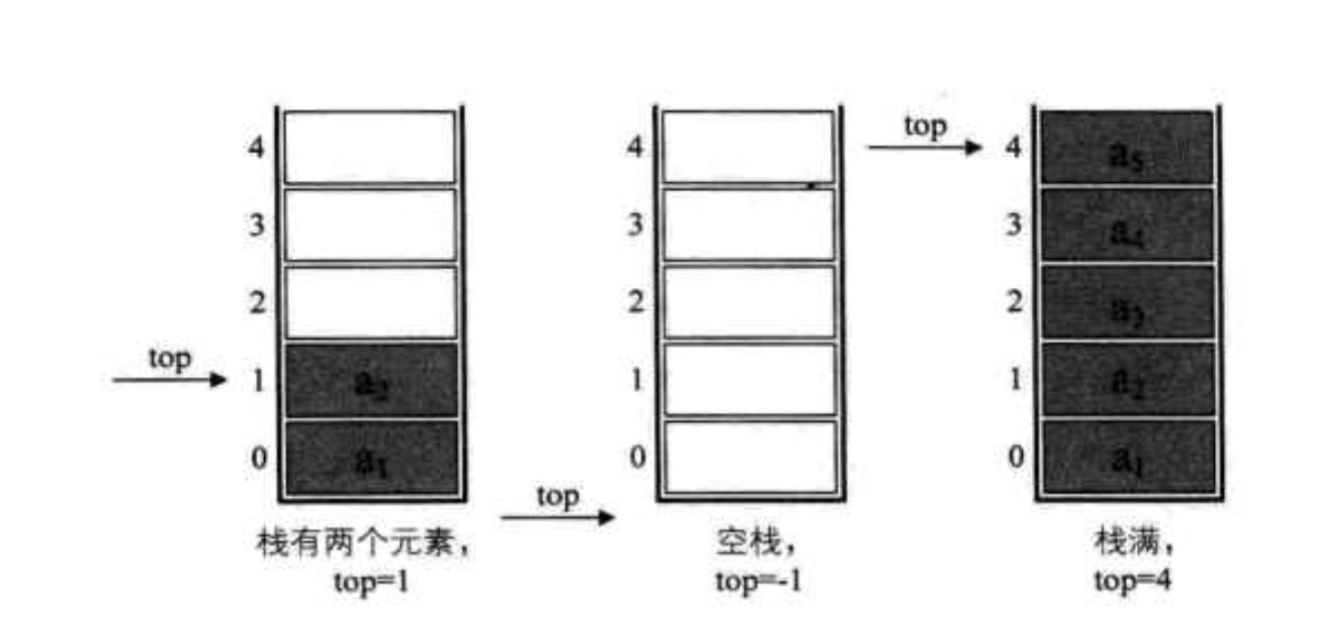
我们把允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom) ,不包含任何数据元素的栈称为空栈,栈又称为先进后出的线性表,简称LIFO结构。
栈的插入操作:叫做进栈,或压栈、入栈。
栈的删除操作:叫做,出栈,或者弹栈。
栈的结构定义
1 /*栈的结构定义*/
2 typedef int sElemType; //sElemType类型定义为int
3 typedef struct {
4
5 sElemType data[MAXSIZE];
6 int top; /*用于栈顶指针*/
7
8 }SqStack;
入栈操作
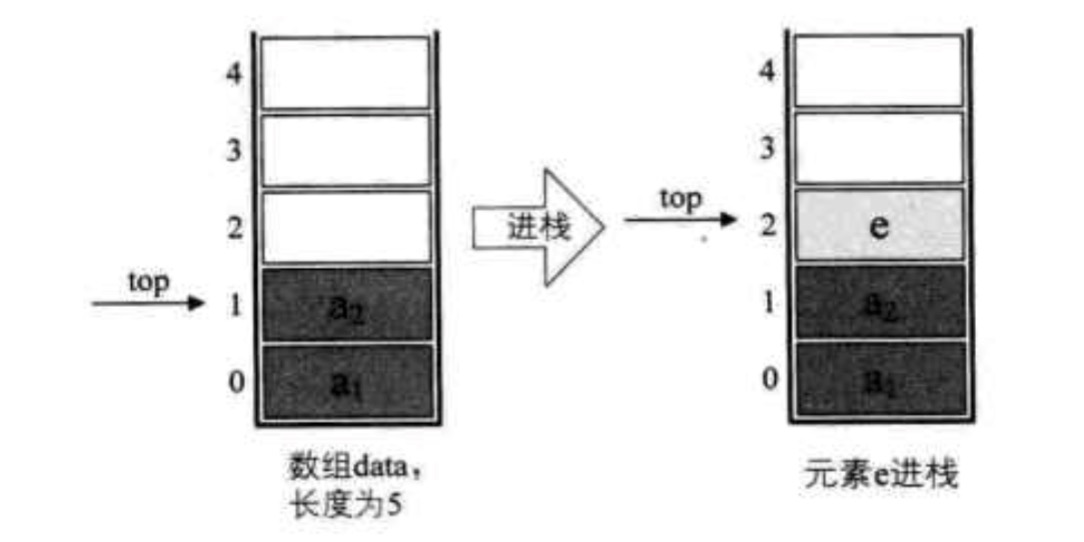
主要代码:
1 /*入栈操作,将元素e入栈*/
2 int PushStack(SqStack* s,sElemType e){
3 //判断入栈的合理性
4 if(s->top == MAXSIZE-1)
5 return 0;
6 s->top++;
7 s->data[s->top]=e;
8 return 1;
9 }
出栈操作
主要代码:
1 /*出栈操作,并用e返回栈顶元素的值*/
2 int PopStack(SqStack* s){
3
4 sElemType e;
5 if((s->top)<0) /*空栈*/
6 return 0;
7 e=s->data[s->top];
8 s->top--;
9 return e;
10 }
用栈之前确记要记得初始化一下
/*栈的初始化*/
void InitStack(SqStack* s){
s->top =0;
}
实现代码

1 #include <stdio.h> 2 3 #define MAXSIZE 20 4 /*栈的结构定义*/ 5 typedef int sElemType; //sElemType类型定义为int 6 7 typedef struct { 8 9 sElemType data[MAXSIZE]; 10 int top; /*用于栈顶指针*/ 11 12 }SqStack; 13 14 /*栈的初始化*/ 15 void InitStack(SqStack* s){ 16 17 s->top =0; 18 } 19 20 /*入栈操作,将元素e入栈*/ 21 int PushStack(SqStack* s,sElemType e){ 22 //判断入栈的合理性 23 if(s->top == MAXSIZE-1) 24 return 0; 25 s->top++; 26 s->data[s->top]=e; 27 return 1; 28 } 29 30 /*出栈操作,并用e返回栈顶元素的值*/ 31 int PopStack(SqStack* s){ 32 33 sElemType e; 34 if((s->top)<0) /*空栈*/ 35 return 0; 36 37 e=s->data[s->top]; 38 s->top--; 39 return e; 40 } 41 42 int main(){ 43 SqStack stack; 44 InitStack(&stack); 45 PushStack(&stack,100); 46 int pop=PopStack(&stack); 47 printf("出栈数据:%d ",pop); 48 49 return 0; 50 }
Java代码

1 package stackdemo; 2 3 public class TestStack { 4 5 public static void main(String[] args) { 6 7 SqeStack s = new SqeStack(); 8 s.initStack(s); 9 s.pushStack(s, 10); 10 int pop = s.popStack(s); 11 System.out.println("出栈数据: " + pop); 12 } 13 14 }

1 package stackdemo; 2 3 public class SqeStack { 4 5 int top; // 栈元素个数 6 int data[] = new int[20]; 7 8 /** 9 * 栈的初始化 10 */ 11 public void initStack(SqeStack s) { 12 s.top = 0; 13 } 14 15 /** 16 * 进栈操作,n进栈数据 17 */ 18 int pushStack(SqeStack s, int n) { 19 if (s.top == 19) 20 return 0; 21 s.top++; 22 s.data[s.top] = n; 23 return 1; 24 } 25 26 /** 27 * 出栈操作 28 */ 29 int popStack(SqeStack s) { 30 int e; 31 if (s.top == 0) 32 return 0; 33 e = s.data[s.top]; 34 s.top--; 35 return e; 36 } 37 38 }
完毕 - -
