常见的三种插入排序

1、直接插入排序算法

直接插入排序的基本操作是将一个记录插到已排队好的有序表中，从而得到一个新的，记录增1的有序表。

// 直接插入排序.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "stdio.h"
//直接插入排序
void InsertSort(int a[], int len);
 void main(){
     int i;
    int a[5] = {5,3,4,6,2};
    InsertSort(a,5);

    for (i = 0; i < 5; i++)
        printf("%d ", a[i]);
}

void InsertSort(int a[] ,int len){
    int temp,i,j;
    for (i = 1; i < len;i++)
    {
        if (a[i] < a[i - 1]){
            temp = a[i];          //用一个临时变量存一下
                for (j = i - 1; a[j] > temp && j>=0; j--){
                    a[j + 1] = a[j];                   //凡事比i这个数大的就要后移，因为大的数总是在后面
                }
                a[j+1] = temp;   //这里需要注意的是j+1，调bug好累勒  ->@@
        }
    }
}

直接插入排序算法分析

根据代码我们来解释一下直接插入排序的核心

例如，我们要对5,3,4,6,2这几个数进行排序

a[]	0	1	2	3	4
值	5	3	4	6	2

当这个数组进入函数后，下标首先定义到i = 1，即排序前，首先定义为a[0] = 5即是有序的。

进入循环内，比较a[1] 是否小于 a[0] 发现是小于的，这个时候按理说是要把a[0]这个元素右移动1位。然后将a[1]这个元素插在a[0]的位置上

但是考虑到这样子将覆盖原来的a[1]的值，所以先将a[1]的值拷贝一份给temp，然后将a[0]右移一位，再将temp的值传给a[0] .即

a[]	0	1	2	3	4
值	3	5	4	6	2

这时i =2了。此时a[0],a[1]属于有序的序列了，我们此时再次比较a[2]是否小于a[1]（前一位），4<5，满足if条件

temp = a[2] 先拷贝一份，再将a[1] 右移一位，再次比较a[0]是否大于temp ,发现3并没有大于4，由此可见只要i前面有序数存在大于a[i]的值，有序序列就要向后移动，

然后再把a[i] 插在正确的位置。

a[]	0	1	2	3	4
值	3	4	5	6	2

当i = 3时，这个时候6比5大，不满足if条件，也可以发现，前面已经都是有序序列{3,4,5,6}.

a[]	0	1	2	3	4
值	3	4	5	6	2

 

 

最后当i = 4时，发现2 < a[3] 这个时候同理前面操作，先将a[4]拷贝一份给temp ,a[4] = a[3],右移一位

再次比较 ,发现temp < a[2] , a[3] =a[2] ,右移一位

再次比较 ,发现temp < a[1] , a[2] =a[1] ,右移一位

再次比较 ,发现temp < a[0] , a[1] =a[0] ,右移一位

此时就可以把temp 赋值给了a[0] ，这个时候就已经排序完成了。

a[]	0	1	2	3	4
值	2	3	4	5	6

直接插入排序复杂度分析

从空间上看，它只需要一个辅助空间temp ，因此我们关键看它的时间复杂度。

当最好的情况下，也就是序列本身就是有序的 ，这个时候我们只有进行每次的if判断(第20行)，比较的次数n-1,移动的次数0，这个时候时间复杂度O(n)

如果排序记录是随机的话，那么根据概率相同的情况原则，平均比较和移动的次数约为(n^2)/4 次，因此我们可以得出直接插入排序法的书剑复杂度为O(n^2) 从这里也可以看出

直接插入排序比冒泡排序和简单选择排序性能要好一点，是一个稳定的排序算法。

2、折半插入排序算法

折半插入排序（Binary Insertion Sort）是对插入排序算法的一种改进，所谓排序算法过程，就是不断的依次将元素插入前面已排好序的序列中。

基本思想：

基本思想和直接插入排序相同

不同在于查找插入位置

直接插入排序是采用顺序查找法，而折半插入排序排序是采用二分查找思想。

#include <stdio.h>

void BlnInsertSort(int a[], int len);
int main(){

    int i;
    int a[5] = { 15, 3, 41, -6, 2 };
    BlnInsertSort(a, 5);

    for (i = 0; i < 5; i++)
        printf("%d ", a[i]);

    return 0;
}

void BlnInsertSort(int a[], int len){
    int i, temp, j;
    for (i = 1; i < len;i++)
    {
        temp = a[i];　　　／／将要插入的元素拷贝一份
        int low , high,mid;
            low = 0, high = i-1;
            while (low <=high)　　／／在［ｌ．．．ｈ］　中寻找插入的位置
            {
                mid = (low + high) / 2;  //折半
                if (mid <= temp)
                {
                    low = mid+1;     //插在高半区 
                }
                else{
                    high = mid-1;    //插在低半区
                }
            }
            for (j = i - 1; j >= high + 1;--j) //腾出high+1的位置
            {
                a[j + 1] = a[j];   //记录后移
            }
            a[j + 1] = temp;

    }
}

假如要将i 位置上的数插入前面的有序[0...4]序列中，令 i = 5,h =i-1 ,l = 0, m = (h+l)/2;

 发现 i = 5 对应的数 小于 m 对应的数，这个时候 h =m -1 ,查找位置缩小到左半区间 ，m = (h+l)/2;

 

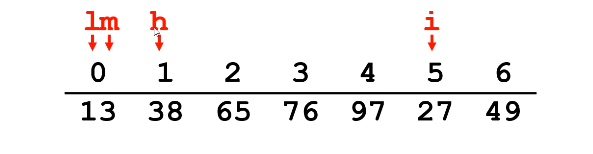
再次比较m 和 i对应的值，发现27 > 13 ,此时发现27应该在m的右半部分。于是 l = m+1 ,m = (h+l)/2;

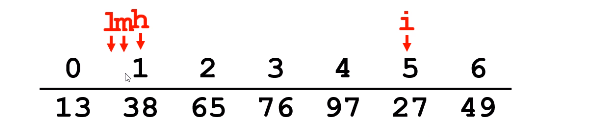
再次比较m 和 i 对应的值，发现27 < 38 ,此时发现27应该在m的左半部分。于是 h = m-1 ,m = (h+l)/2;

 

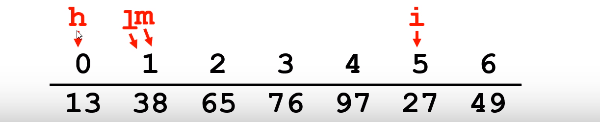
此时再次观察发现h <ｌ这个时候循环就应该结束了。我们ｉ要插入的位置即是　ｈ＋１　，于是将数组元素开始移动，腾出位置，准备插入数据。

这就是二分插入排序的基本思想。

折半插入排序算法复杂度分析

1、折半插入排序要比直接插入排序快，所以折半插入排序的平均性能要优于直接插入排序。

2、折半插入排序的关键码比较次数和待排序序列的初始序列无关，仅依赖于对象的个数，再插入第i个对象时，需要经过{log2 i}次关键码比较，才能确定它插入的位置。

3、当n比较大时，总关键码的比较次数要比直接插入排序情况好的多，但要比最好的情况差。

4、在对象的初始排序已经按关键码排好或接近有序时，直接插入排序比折半插入排序的关键码的比较次数要少。

5、折半插入排序的对象的移动次数与直接插入排序相同，依赖于对象的初始序列，折半插入排序只是在数据较多的情况下减少了比较次数。

3、希尔排序算法

希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。

该方法因D.L.Shell于1959年提出而得名。

基本思想:先将整个待排记录序列分割成若干个子序列，分别进行直接插入排序，待整个序列中的记录 “基本有序” 时，再对全体记录进行一次直接插入排序。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。【百度百科】

看着晦涩的描述有点不好理解，我们来看看具体是怎么操作的。

 

 

用一个变量dk = 5 ,将全部序列分割成

这里要做的事将a[0] ,a[5] ,a[10]；a[1] ,a[6] ,a[11] ；a[2] ,a[7] ,a[12]；a[3] ,a[8] 这几组数做直接插入排序，注意此时的间隔为5，而不是之前的1，完成后

 

发现规律 ，只要是间隔5的每一组数都是有序的，如{35，41，81}，{17,75,91}，{11,15,95}都是有序的，这也导致了全部的序列有序性有所提高。

继续我们现在另dk = 3 ，即将上面的序列分割成间隔为3的子序列，看颜色区分

同理按照5间隔的规则进行排序，排序完后

这个时候有序性又提高了不少。最后再将所有的序列做最后一次的直接插入排序，dk = 1的排序。

直接插入排序在序列元素少，序列的有序性好的情况下，它的效率是非常高的。

 

这个时候就已经全部排序完成了。

代码：

#include<stdio.h>

void ShellSort(int a[], int dk[],int len);
void InsertSort(int a[], int dk, int len);

int main(){

    int i, j, len;
    int a[13] = { 81, 94, 11, 96, 12, 35, 17, 95, 28, 58, 41, 75, 15 };
    int dk[3] = { 0 };
    len = sizeof(a) / 4;
    int increament = len / 3 + 1;  //increament = 5
    for (j = increament, i = 0; j >= 1; j -= 2, i++)  //dk[0...i-1]={5,3,1}
        dk[i] = j;

    ShellSort(a, dk, len);

    printf("排完序：
");
    for (i = 0; i < len; i++)
        printf("%d ", a[i]);
    printf("
");

    return 0;
}

void ShellSort(int a[], int dk[],int len){
    int i,j=0;
    //按增量序列dk[0...i-1]对顺序表进行希尔排序
    for (i = 0; i < 3; i++){
        printf("第%d趟排序: ",++j );
        InsertSort(a, dk[i], len);   //一趟增量为dk[i]的插入排序
    }
}

void InsertSort(int a[], int dk,int len){

    int i, j, temp;
    for (i = dk; i < len; i++){
        if (a[i] < a[i - dk]){
            temp = a[i];
            //从有往左开始扫描，寻找有没有大于temp的数(间隔是dk)
            for (j = i - dk; j >= 0 && (temp < a[j]); j = j - dk){
                a[j + dk] = a[j];
            }
            a[j + dk] = temp;
        }
    }
    //输出每一趟排序结果
    for (i = 0; i < len; i++)
        printf("%d ", a[i]);
    printf("
");
}

 希尔排序的特点：

1、一次移动，移动位置较大，跳跃式接近排序后的最终位置。

2、最后一次只需要进行少量的移动。

3、增量序列必须是递减的，最后一个必须是1.

4、增量序列应该是互质的。

希尔排序算法的复杂度分析

希尔排序算法的效率和增量序列的取值有关系

那么增量序列是如何取值的，取一些什么值才能达到最高的排序效率呢？

这个问题至今都没有被解决，是一个数学上的难题。

大量研究表明增量序列为：

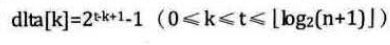
可以获得不错的效率，其时间复杂度为O(n^2/3).要优于直接插入排序的O(n^2) 

需要注意的是，最后一个增量必须是1才可以。由于记录是跳跃性移动的，所以希尔排序并不是一个稳定的排序算法。

常见的内部排序就这3个，严奶奶书里面还提到了2-路插入排序表插入排序。

 如果有些错的地方大家希望可以指出，我们共同进步 -- 共勉之**

参考资料：《大话数据结构》

https://www.bilibili.com/video/av38482403/?spm_id_from=333.788.videocard.5

https://www.bilibili.com/video/av43523066/?p=2