Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 129 Accepted Submission(s): 59
Problem Description
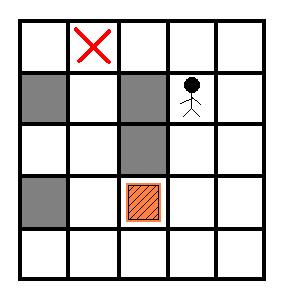
推箱子是一个很经典的游戏.今天我们来玩一个简单版本.在一个M*N的房间里有一个箱子和一个搬运工,搬运工的工作就是把箱子推到指定的位置,注意,搬运工只能推箱子而不能拉箱子,因此如果箱子被推到一个角上(如图2)那么箱子就不能再被移动了,如果箱子被推到一面墙上,那么箱子只能沿着墙移动.
现在给定房间的结构,箱子的位置,搬运工的位置和箱子要被推去的位置,请你计算出搬运工至少要推动箱子多少格.
Input
输入数据的第一行是一个整数T(1<=T<=20),代表测试数据的数量.然后是T组测试数据,每组测试数据的第一行是两个正整数M,N(2<=M,N<=7),代表房间的大小,然后是一个M行N列的矩阵,代表房间的布局,其中0代表空的地板,1代表墙,2代表箱子的起始位置,3代表箱子要被推去的位置,4代表搬运工的起始位置.
Output
对于每组测试数据,输出搬运工最少需要推动箱子多少格才能帮箱子推到指定位置,如果不能推到指定位置则输出-1.
Sample Input
1 5 5 0 3 0 0 0 1 0 1 4 0 0 0 1 0 0 1 0 2 0 0 0 0 0 0 0
Sample Output
4
Author
Ignatius.L & weigang Lee
Recommend
Ignatius.L
思路:
如果没有人,这看箱子的话,这是一个简单的BFS
但是,这道题目另一个限制因素:人。有的箱子位置是人推不到的
所以我们在BFS箱子位置的同时,也要搜索人的位置(能否到达箱子的相反位置),这里我用的DFS写的
有一个需要注意的点:
箱子可以走回头路
例如如下样例:
5 5
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 2 1 1 4 0 3 0 0
若直接去掉标记数组当然可以解决,但这样的话铁定超时
另一个方法是使用一个三维的标记数组,分别记录箱子的位置与人的位置
代码如下:
#include<bits/stdc++.h> using namespace std; int m[10][10]; bool vis[10][10][4]; bool vi[10][10]; int M,N; int endx,endy; int dfsx,dfsy; int dir[4][2]= {{1,0},{-1,0},{0,1},{0,-1}}; int to[4][2]={{-1,0},{1,0},{0,-1},{0,1}}; struct node { int x1,y1;//箱子所在位置 int x2,y2;//人所在位置 int step; void print(){ cout<<"step:"<<step<<" "<<x1+1<<" "<<y1+1<<" "<<x2+1<<" "<<y2+1<<endl; } }; int DFS(int rx,int ry) { if(rx==dfsx&&ry==dfsy) { return 1; } vi[rx][ry]=1; for(int i=0;i<4;i++){ int xx=rx+dir[i][0];int yy=ry+dir[i][1]; if(xx<0||xx>=M||yy<0||yy>=N||m[xx][yy]!=0||vi[xx][yy]) continue; if(DFS(xx,yy)) { return 1; } }
return 0; } queue<node> q; int BFS(node b) { memset(vis,0,sizeof(vis)); while(!q.empty()){ q.pop(); } q.push(b); node tmp,t; while(!q.empty()){ t=q.front(); q.pop(); //cout<<"out"<<" ";t.print(); if(t.x1==endx&&t.y1==endy) return t.step; for(int i=0;i<4;i++){ tmp=t; tmp.step++; tmp.x1+=dir[i][0]; tmp.y1+=dir[i][1]; if(vis[t.x1][t.y1][i]==0&&tmp.x1>=0&&tmp.x1<M&&tmp.y1>=0&&tmp.y1<N&&m[tmp.x1][tmp.y1]==0){ memset(vi,0,sizeof(vi)); vi[tmp.x2][tmp.y2]=1; dfsx=t.x1+to[i][0];dfsy=t.y1+to[i][1]; m[t.x1][t.y1]=2; if(DFS(t.x2,t.y2)){ vis[t.x1][t.y1][i]=1; tmp.x2=t.x1,tmp.y2=t.y1; q.push(tmp); //cout<<q.size()<<" "<<"in"<<" ";tmp.print(); } m[t.x1][t.y1]=0; } } } return -1; } int main() { //freopen("data.in","r",stdin); int t; //cin>>t; scanf("%d",&t); int x,y; while(t--){ memset(m,-1,sizeof(m)); //cin>>M>>N; scanf("%d%d",&M,&N); for(int i=0;i<M;i++){ for(int j=0;j<N;j++){ //cin>>m[i][j]; scanf("%d",&m[i][j]); } } node b; b.step=0; for(int i=0;i<M;i++){ for(int j=0;j<N;j++){ if(m[i][j]==2) {b.x1=i,b.y1=j;m[i][j]=0;} if(m[i][j]==4) {b.x2=i,b.y2=j;m[i][j]=0;} if(m[i][j]==3) {endx=i,endy=j;m[i][j]=0;} } } cout<<BFS(b)<<endl; } }