目录
1 问题描述
设计一种策略,使在下面的游戏中,期望提问的次数达到最小。有一副纸牌,是由1张A,2张2,3张3,...9张9组成的,一共包含45张牌。有人从这副牌洗过的牌中抽出一张牌,问一连串可以回答是或否的问题来确定这副牌的点数。
2 解决方案
2.1 贪婪法原理简介
贪婪法的核心是,所做的每一步选择都必须满足以下条件:
(1)可行的:即它必须满足问题的约束。
(2)局部最优:它是当前步骤中所有可行选择中最佳的局部选择。
(3)不可取消:即选择一旦做出,在算法的后面步骤中就无法改变了。
这些条件即要求:在每一步中,它要求“贪婪”地选择最佳操作,并希望通过一系列局部的最优选择,能够产生一个整个问题的(全局的)最优解。
2.2 哈夫曼树及编码简介
哈夫曼树,树中所有的左向边都标记为0,而所有的右向边都标记为1.可以通过记录从根到字符叶子的简单路径上的标记来获得一个字符的哈夫曼编码。
示例:
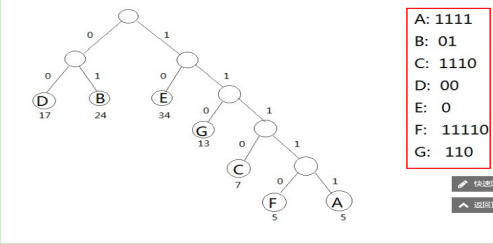
要了解哈夫曼树,首先了解一下哈夫曼算法,哈夫曼算法满足以下两步:
第一步:初始化n个单节点的树,并为它们标上字母表中的字符。把每个字符的概率记在树的根节点中,用来指出树的权重(更一般地来说,树的权重等于树中所有叶子节点的概率之和)。
第二步:重复下面的步骤,直到只剩下一棵单独的树。找到两棵权重最小的树(如果权重相同,则任意选取其一)。把它们作为新树中的左右子树,并把其权重之和作为新的权重记录在新树的根节点中。
示例:
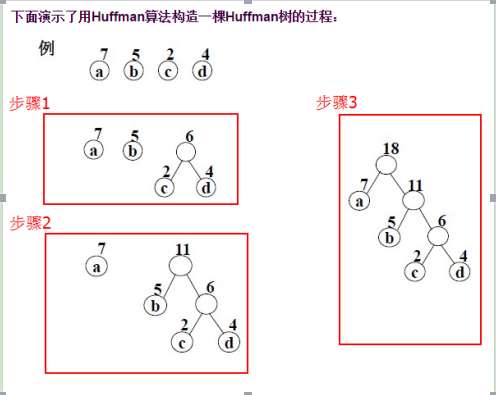
树的带权路径长度:如果树中每个叶子上都带有一个权值,则把树中所有叶子的带权路径长度之和称为树的带权路径长度。
设某二叉树有n个带权值的叶子结点,则该二叉树的带权路径长度记为:
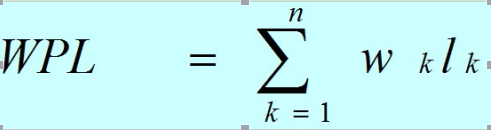
公式中,Wk为第k个叶子结点的权值;Lk为该结点的路径长度。
示例:
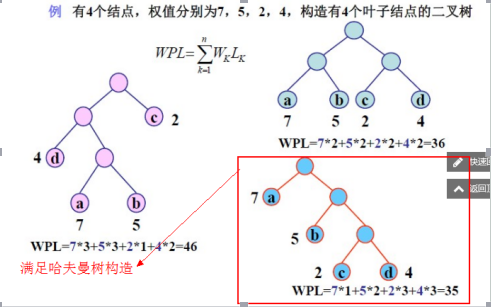
2.3 具体编码
针对猜底牌问题,此处需要构建哈夫曼树,通过哈夫曼编码的长度来确定具体回答是或否的个数。此处把哈夫曼编码中的0代表回答否,1代表回答是,根据哈夫曼编码中的0或者1的总个数来确定提问的次数。
首先,创建一个树的节点类:
package com.liuzhen.huffman; /*定义一个Node类,其类型为T(PS:即在初始化时自行选择相关数据类型),该类用于定义哈夫曼树中一个节点的类型 * 该类并实现Compareble接口 * Compareble接口强行对实现它的每个类的对象进行整体排序。此排序被称为该类的自然排序 ,类的 compareTo 方法被称为它的自然比较方法 。 * 实现此接口的对象列表(和数组)可以通过 Collections.sort (或Arrays.sort )进行自动排序。 */ public class Node<T> implements Comparable<Node<T>> { private T data; //二叉树节点的名称 private int weight; //二叉树节点的权重 private Node<T> left; //节点的左孩子 private Node<T> right; //节点的右孩子 private String code = ""; //二叉树节点的哈夫曼编码,初始化为空 //构造函数 public Node(T data, int weight) { this.data = data; this.weight = weight; } /* * toString的好处是在碰到“println”之类的输出方法时会自动调用,不用显式打出来 * 它是Object里面已经有了的方法,此处将该方法进行重写 * 它通常只是为了方便输出,比如System.out.println(xx),括号里面的“xx”如果不是String类型的话, * 就自动调用xx的toString()方法 * 此处就可以输出一个Node类对象时,直接输出toString()方法体中返回的字符串 */ @Override public String toString() { return "data:" + this.data + ",weight:" + this.weight +",code:"+this.code+ "; "; } @Override public int compareTo(Node<T> o) { //此处实现Compareble接口中方法compaerto,对Node类对象进行从大到小排序 if (o.weight > this.weight) { return 1; } else if (o.weight < this.weight) { return -1; } return 0; } public T getData() { return data; } public void setData(T data) { this.data = data; } public int getWeight() { return weight; } public void setWeight(int weight) { this.weight = weight; } public String getCode() { return code; } public void setCode(String code) { this.code = code; } public Node<T> getLeft() { return left; } public void setLeft(Node<T> left) { this.left = left; } public Node<T> getRight() { return right; } public void setRight(Node<T> right) { this.right = right; } }
其次,创建一个用于构建哈夫曼树和输出哈夫曼树的类:
package com.liuzhen.huffman; import java.util.*; public class HuffmanTree<T> { //构建哈夫曼树方法,其返回类型为Node<T> public static <T> Node<T> createTree(List<Node<T>> nodes) { while (nodes.size() > 1) { Collections.sort(nodes); //调用Node<T>类中实现接口的排序方法,对节点对象进行从大到小排序 Node<T> left = nodes.get(nodes.size() - 1); //获取链表中最小的元素,作为左孩子 Node<T> right = nodes.get(nodes.size() - 2); //获取链表中第二小的元素,作为右孩子 Node<T> parent = new Node<T>(null, left.getWeight() + right.getWeight()); //左孩子和右孩子权重相加的和,作为其父节点 parent.setLeft(left); parent.setRight(right); nodes.remove(left); nodes.remove(right); nodes.add(parent); //将父节点加入链表中 } return nodes.get(0); } //使用广度优先遍历法,返回哈夫曼树的结果队列 public static <T> List<Node<T>> breath(Node<T> root) { //定义最终返回的结果队列 List<Node<T>> list = new ArrayList<Node<T>>(); /*Queue(队列)特性是先进先出,队尾插入,队首删除 * Queue使用时要尽量避免Collection的add()和remove()方法,而是要 * 使用offer()来加入元素,使用poll()来获取并移除元素 * LinkedList类实现了Queue接口,因此,可以把LinkedList当成Queue来使用 */ Queue<Node<T>> queue = new LinkedList<>(); // root.setCode(""); //哈夫曼树根节点的哈夫曼编码设定为空字符串“” queue.offer(root); while (!queue.isEmpty()) { Node<T> pNode = queue.poll(); //使用poll()来获取并移除元素 list.add(pNode); if (pNode.getLeft() != null) { String code = pNode.getCode(); //获取父节点的哈夫曼编码 code += "0"; //左孩子的哈夫曼编码加字符串“0” pNode.getLeft().setCode(code); queue.offer(pNode.getLeft()); //使用offer()来加入元素 } if (pNode.getRight() != null) { String code = pNode.getCode(); //获取父节点的哈夫曼编码 code += "1"; //右孩子的哈夫曼编码加字符串“1” pNode.getRight().setCode(code); queue.offer(pNode.getRight()); } } return list; } }
最后,输入题目中数据(对于题目的A,1,...,9,我分别取代号为字母A,B,C,...,其张数的大小即为哈夫曼树中相应节点的权重),得到输出最终结果:
package com.liuzhen.huffman; import java.util.*; public class HuffmanTreeTest { public static void main(String[] args) { // TODO Auto-generated method stub List<Node<String>> nodes = new ArrayList<Node<String>>(); nodes.add(new Node<String>("A", 1)); nodes.add(new Node<String>("B", 2)); nodes.add(new Node<String>("C", 3)); nodes.add(new Node<String>("D", 4)); nodes.add(new Node<String>("E", 5)); nodes.add(new Node<String>("F", 6)); nodes.add(new Node<String>("G", 7)); nodes.add(new Node<String>("H", 8)); nodes.add(new Node<String>("I", 9)); Node<String> root = HuffmanTree.createTree(nodes); System.out.println(HuffmanTree.breath(root)); } }
2.4 运行结果
[data:null,weight:45,code:; , data:null,weight:18,code:0; , data:null,weight:27,code:1; , data:null,weight:9,code:00; , data:I,weight:9,code:01; , data:null,weight:12,code:10; , data:null,weight:15,code:11; , data:D,weight:4,code:000; , data:E,weight:5,code:001; , data:null,weight:6,code:100; , data:F,weight:6,code:101; , data:G,weight:7,code:110; , data:H,weight:8,code:111; , data:null,weight:3,code:1000; , data:C,weight:3,code:1001; , data:A,weight:1,code:10000; , data:B,weight:2,code:10001; ]
参考资料:
1、哈夫曼树