目录
1 问题描述
何为Prim算法?
此处引用网友博客中一段介绍(PS:个人感觉网友的这篇博客对于Prim算法讲解的很清楚,本文与之相区别的地方在于具体实现代码的不同,该网友是使用C++实现,而本文是使用Java实现。其他理论讲解可以参考该网友的博客哦,具体链接看文末参考资料)
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克(英语:Vojtěch Jarník)发现;并在1957年由美国计算机科学家罗伯特·普里姆(英语:Robert C. Prim)独立发现;1959年,艾兹格·迪科斯彻再次发现了该算法。因此,在某些场合,普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆-亚尔尼克算法。
原理简单介绍:
1).输入:一个加权连通图,其中顶点集合为V,边集合为E;
2).初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
3).重复下列操作,直到Vnew = V:
a.在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
b.将v加入集合Vnew中,将<u, v>边加入集合Enew中;
4).输出:使用集合Vnew和Enew来描述所得到的最小生成树。
2 解决方案
2.1 贪心法
本文具体编码使用数据参考自《算法设计与分析基础》第三版,下面是其具体图示:
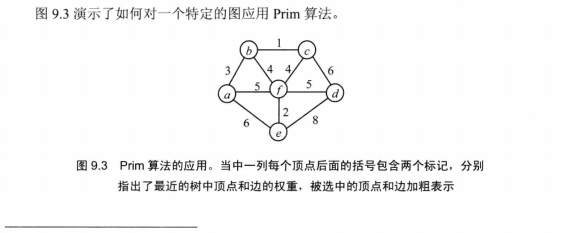
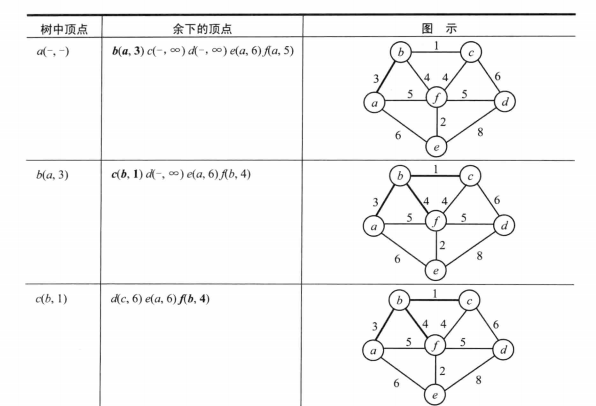

具体代码如下:
package com.liuzhen.chapter8; import java.util.ArrayList; public class Prim { /* * 参数G:给定的图,其顶点分别为0~G.length-1,相应权值为具体元素的值 * 函数功能:返回构造生成的最小生成树,以二维数组形式表示,其中元素为0表示最小生成树的边 */ public void getMinTree(int[][] G) { int[][] result = G; int[] vertix = new int[G.length]; //记录顶点是否被访问,如果已被访问,则置相应顶点的元素值为-2 for(int i = 0;i < G.length;i++) vertix[i] = i; ArrayList<Integer> listV = new ArrayList<Integer>(); //保存已经遍历过的顶点 listV.add(0); //初始随意选择一个顶点作为起始点,此处选择顶点0 vertix[0] = -2; //表示顶点0被访问 while(listV.size() < G.length) { //当已被遍历的顶点数等于给定顶点数时,退出循环 int minDistance = Integer.MAX_VALUE; //用于寻找最小权值,初始化为int最大值,相当于无穷大的意思 int minV = -1; //用于存放未被遍历的顶点中与已被遍历顶点有最小权值的顶点 int minI = -1; //用于存放已被遍历的顶点与未被遍历顶点有最小权值的顶点 ;即G[minI][minV]在剩余的权值中最小 for(int i = 0;i < listV.size();i++) { //i 表示已被访问的顶点 int v1 = listV.get(i); for(int j = 0;j < G.length;j++) { if(vertix[j] != -2) { //满足此条件的表示,顶点j未被访问 if(G[v1][j] != -1 && G[v1][j] < minDistance) {//G[v1][j]值为-1表示v1和j是非相邻顶点 minDistance = G[v1][j]; minV = j; minI = v1; } } } } vertix[minV] = -2; listV.add(minV); result[minI][minV] = 0; result[minV][minI] = 0; } System.out.println("使用Prim算法,对于给定图中的顶点访问顺序为:"); System.out.println(listV); System.out.println("使用Prim算法,构造的最小生成树的二维数组表示如下(PS:元素为0表示树的边):"); for(int i = 0;i < result.length;i++) { for(int j = 0;j < result[0].length;j++) System.out.print(result[i][j]+" "); System.out.println(); } } public static void main(String[] args) { Prim test = new Prim(); int[][] G = {{-1,3,-1,-1,6,5}, {3,-1,1,-1,-1,4}, {-1,1,-1,6,-1,4}, {-1,-1,6,-1,8,5}, {6,-1,-1,8,-1,2}, {5,4,4,5,2,-1}}; test.getMinTree(G); } }
运行结果:
使用Prim算法,对于给定图中的顶点访问顺序为: [0, 1, 2, 5, 4, 3] 使用Prim算法,构造的最小生成树的二维数组表示如下(PS:元素为0表示树的边): -1 0 -1 -1 6 5 0 -1 0 -1 -1 0 -1 0 -1 6 -1 4 -1 -1 6 -1 8 0 6 -1 -1 8 -1 0 5 0 4 0 0 -1
参考资料:
1.《算法设计与分析基础》第3版 Anany Levitin 著 潘彦 译