目录
1 问题描述
有n个格子,从左到右放成一排,编号为1-n。
共有m次操作,有3种操作类型:
1.修改一个格子的权值,
2.求连续一段格子权值和,
3.求连续一段格子的最大值。
对于每个2、3操作输出你所求出的结果。
第一行2个整数n,m。
接下来一行n个整数表示n个格子的初始权值。
接下来m行,每行3个整数p,x,y,p表示操作类型,p=1时表示修改格子x的权值为y,p=2时表示求区间[x,y]内格子权值和,p=3时表示求区间[x,y]内格子最大的权值。
有若干行,行数等于p=2或3的操作总数。
每行1个整数,对应了每个p=2或3操作的结果。
1 2 3 4
2 1 3
1 4 3
3 1 4
3
对于20%的数据n <= 100,m <= 200。
对于50%的数据n <= 5000,m <= 5000。
对于100%的数据1 <= n <= 100000,m <= 100000,0 <= 格子权值 <= 10000。
2 解决方案
花了一上午的时间把线段树整明白,然后把写好的代码放到蓝桥杯练习系统里面测试时,运行结果依旧是超时,而且我用同样的代码反复提交了三四次,分数也都竟然都不一样,分别是30,40,50。我也是无语了...
虽然这题没能得到100分,我猜测可能与Java和C/C++语言之间的编译运行性能有关,导致用同样的方法,Java语言运行时间要长的多。
如果有哪位同学看出下面的代码不是语言之间的差异,而是楼主我自己的代码问题,还希望路过的同学不吝赐教呀~
关于线段树,具体的理解可以参考文末的参考资料,参考资料给的文章个人感觉对于线段树的讲解很清楚,唯一的不足之处是文中对于完全二叉树的概念理解有点错误,但是不影响我们对于线段树的理解哦。
下面附一点该文章对于线段树的概念介绍:
线段树,类似区间树,它在各个节点保存一条线段(数组中的一段子数组),主要用于高效解决连续区间的动态查询问题,由于二叉结构的特性,它基本能保持每个操作的复杂度为O(logn)。
线段树的每个节点表示一个区间,子节点则分别表示父节点的左右半区间,例如父亲的区间是[a,b],那么(c=(a+b)/2)左儿子的区间是[a,c],右儿子的区间是[c+1,b]。
构造线段树示例:
例如对于数组[2, 5, 1, 4, 9, 3]可以构造如下的二叉树(背景为白色表示叶子节点,非叶子节点的值是其对应数组区间内的最小值,例如根节点表示数组区间arr[0...5]内的最小值是1):
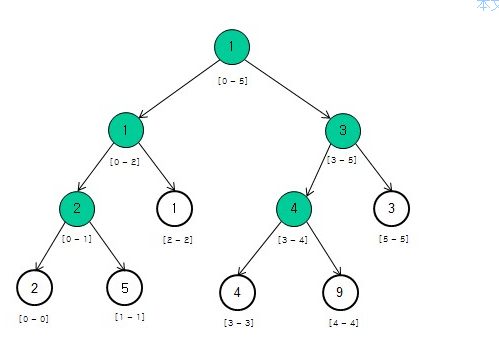
下面请看具体代码:
package com.liuzhen.systemExe; import java.util.Scanner; public class Main{ public int[][] segTree; /* * 参数root:代表线段树的根节点,此处使用数组存放线段树,其根节点从0开始计数,那么其两个子节点编号必定满足2*root+1或者2*root+2 * 参数array:给定的目标数组,需要转成相应功能的线段树 * 参数start:线段树划分给定数组区间的起始位置 * 参数end:线段树划分给定数组区间的末尾位置 * 函数功能:返回一个线段树,其所有节点均存放当前数组子区间内的总和以及最大值 */ public void buildSegTree(int root, int[] array, int start, int end) { if(start == end) { segTree[root][0] = array[start]; segTree[root][1] = array[start]; } else { int mid = (start + end) / 2; buildSegTree(2 * root + 1, array, start, mid); //递归构造左半子树 buildSegTree(2 * root + 2, array, mid + 1, end); //递归构造右半子树 segTree[root][0] = (segTree[2*root+1][0] > segTree[2*root+2][0] ? segTree[2*root+1][0] : segTree[2*root+2][0]); //回溯求取当前节点区间存放的元素最大值 segTree[root][1] = segTree[root*2+1][1] + segTree[root*2+2][1]; //回溯求取当前节点区间存放的元素总和 } } /* * 参数root:开始进行查找的根节点对应的数组下标值 * 参数start-end:当前节点所表示的区间 * 参数qstart-qend:此次查询的区间 * 函数功能:查询当前区间qstart-qend的最大值 */ public int querySegTreeMax(int root, int start, int end, int qstart, int qend) { if(qstart > end || qend < start) return 0; int max = 0; if(qstart <= start && qend >= end) { return segTree[root][0]; } else { int mid = (start + end) / 2; int temp1 = querySegTreeMax(root * 2 + 1, start, mid, qstart, qend); int temp2 = querySegTreeMax(root * 2 + 2, mid + 1, end, qstart, qend); if(temp1 > temp2) max = temp1; else max = temp2; } return max; } /* * 参数root:开始进行查找的根节点对应的数组下标值 * 参数start-end:当前节点所表示的区间 * 参数qstart-qend:此次查询的区间 * 函数功能:查询当前区间qstart-qend的总和 */ public int querySegTreeSum(int root, int start, int end, int qstart, int qend) { if(qstart > end || qend < start ) return 0; int sum = 0; if(qstart == start && qend == end) { return segTree[root][1]; } else { int mid = (start + end) / 2; if(qstart <= mid && qend > mid) { int temp1 = querySegTreeSum(root * 2 + 1, start, mid, qstart, mid); int temp2 = querySegTreeSum(root * 2 + 2, mid + 1, end, mid + 1, qend); sum = temp1 + temp2; } else if(qstart > mid) { int temp2 = querySegTreeSum(root * 2 + 2, mid + 1, end, qstart, qend); sum = temp2; } else if(qend <= mid) { int temp1 = querySegTreeSum(root * 2 + 1, start, mid, qstart, qend); sum = temp1; } } return sum; } /* * 参数root:开始进行查找的根节点对应的数组下标值 * 参数qstart-qend:当前节点所表示的区间 * 函数功能:把数组下标为index的元素值变成value,并更新线段树 */ public void updateSegTree(int root, int qstart, int qend, int index, int value) { if(qstart == qend) { if(index == qstart) { segTree[root][0] = value; segTree[root][1] = value; } return; } int mid = (qstart + qend) / 2; if(mid >= index) { updateSegTree(root * 2 + 1, qstart, mid, index, value); } else { updateSegTree(root * 2 + 2, mid + 1, qend, index, value); } //回溯更新改变值元素值的根节点相应值 segTree[root][0] = (segTree[root*2+1][0] > segTree[root*2+2][0] ? segTree[root*2+1][0] : segTree[root*2+2][0]); segTree[root][1] = segTree[root*2+1][1] + segTree[root*2+2][1]; } public void printResult(int[] A, int[][] operation) { segTree = new int[4 * A.length][2];//此处初始化线段树行的长度为4 * n,有n个元素的数组构造的线段树其对应的二叉树层数最大可以达到4*n个节点 buildSegTree(0, A, 0, A.length - 1); for(int i = 0;i < operation.length;i++) { if(operation[i][0] == 1) { updateSegTree(0, 0, A.length - 1, operation[i][1] - 1, operation[i][2]); } else if(operation[i][0] == 2) { int sum = querySegTreeSum(0, 0, A.length - 1, operation[i][1] - 1, operation[i][2] - 1); System.out.println(sum); } else if(operation[i][0] == 3) { int max = querySegTreeMax(0, 0, A.length - 1, operation[i][1] - 1, operation[i][2] - 1); System.out.println(max); } } } public static void main(String[] args){ Main test = new Main(); Scanner in = new Scanner(System.in); int n = in.nextInt(); int m = in.nextInt(); if(n >100000 || n <= 0 || m > 100000 || m <= 0) //此处是依据题意给定范围做判断 return; int[] A = new int[n]; for(int i = 0;i < n;i++) A[i] = in.nextInt(); int[][] operation = new int[m][3]; for(int i = 0;i < m;i++) { for(int j = 0;j < 3;j++) { operation[i][j] = in.nextInt(); } } test.printResult(A, operation); } }
参考资料: