目录
1 问题描述
问题描述
斐波那契数列大家都非常熟悉。它的定义是:
f(x) = 1 .... (x=1,2)
f(x) = f(x-1) + f(x-2) .... (x>2)
对于给定的整数 n 和 m,我们希望求出:
f(1) + f(2) + ... + f(n) 的值。但这个值可能非常大,所以我们把它对 f(m) 取模。
公式如下
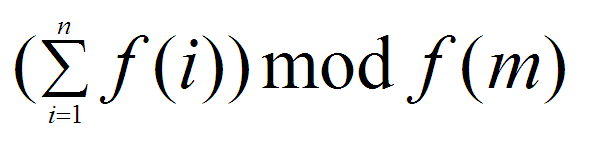
但这个数字依然很大,所以需要再对 p 求模。
f(x) = 1 .... (x=1,2)
f(x) = f(x-1) + f(x-2) .... (x>2)
对于给定的整数 n 和 m,我们希望求出:
f(1) + f(2) + ... + f(n) 的值。但这个值可能非常大,所以我们把它对 f(m) 取模。
公式如下
但这个数字依然很大,所以需要再对 p 求模。
输入格式
输入为一行用空格分开的整数 n m p (0 < n, m, p < 10^18)
输出格式
输出为1个整数,表示答案
样例输入
2 3 5
样例输出
0
样例输入
15 11 29
样例输出
25
2 解决方案
本题代码在蓝桥练习系统中测评为40分,有待优化,下面代码主要运用矩阵幂,可以提高求取斐波那契数的效率,但是依旧不满足测评数据的时间效率。

具体代码如下:
import java.math.BigInteger; import java.util.Scanner; public class Main { public static BigInteger[][] ZERO = {{BigInteger.ZERO,BigInteger.ZERO}, {BigInteger.ZERO,BigInteger.ZERO}}; public static BigInteger[][] KEY = {{BigInteger.ONE,BigInteger.ONE}, {BigInteger.ONE,BigInteger.ZERO}}; public static BigInteger MOD; public BigInteger[][] mergeMulti(long n) { if(n == 0) return ZERO; if(n == 1) return KEY; if((n&1) == 0) { //当n为偶数 BigInteger[][] temp = mergeMulti(n>>1); return matrixMulti(temp, temp); } //当n为奇数 BigInteger[][] temp = mergeMulti(n>>1); return matrixMulti(matrixMulti(temp, temp), KEY); } public BigInteger[][] matrixMulti(BigInteger[][] A, BigInteger[][] B) { BigInteger[][] result = new BigInteger[A.length][B[0].length]; for(int i = 0;i < result.length;i++) for(int j = 0;j < result[0].length;j++) result[i][j] = BigInteger.ZERO; for(int i = 0;i < A.length;i++) for(int j = 0;j < B[0].length;j++) for(int k = 0;k < A[0].length;k++) result[i][j] = result[i][j].add(A[i][k].multiply(B[k][j])); return result; } public BigInteger getResult(long n) { if(n == 1 || n == 2) return BigInteger.ONE; n = n - 2; BigInteger[][] temp = mergeMulti(n); BigInteger[][] value = {{BigInteger.ONE, BigInteger.ONE}}; value = matrixMulti(value, temp); return value[0][0]; } public static void main(String[] args) { Main test = new Main(); Scanner in = new Scanner(System.in); long n = in.nextLong(); long m = in.nextLong(); MOD = in.nextBigInteger(); BigInteger result = test.getResult(n + 2).subtract(BigInteger.ONE); result = result.mod(test.getResult(m)).mod(MOD); System.out.println(result); } }