前言:以下代码部分仅供参考,C语言解答部分全部来自网友,Java语言部分部分参考自网友,对于答案的正确性不能完全保证。
试题1
数论中有著名的四方定理:所有自然数至多只要用四个数的平方和就可以表示。 我们可以通过计算机验证其在有限范围的正确性。 对于大数,简单的循环嵌套是不适宜的。下面的代码给出了一种分解方案。 请仔细阅读,填写空缺的代码(下划线部分)。 注意:请把填空的答案(仅填空处的答案,不包括题面)存入考生文件夹下对应题号的“解答.txt”中即可。 直接写在题面中不能得分。 int f(int n, int a[], int idx) { if(______________) return 1; // 填空1 if(idx==4) return 0; for(int i=(int)sqrt(n); i>=1; i--) { a[idx] = i; if(_______________________) return 1; // 填空2 } return 0; } int main(int argc, char* argv[]) { for(;;) { int number; printf("输入整数(1~10亿):"); scanf("%d",&number); int a[] = {0,0,0,0}; int r = f(number, a, 0); printf("%d: %d %d %d %d ", r, a[0], a[1], a[2], a[3]); } return 0; } a[0]*a[0] + a[1]*a[1] + a[2]*a[2] + a[3]*a[3] == n f(n, a, idx + 1) == 1
来自网友:
本题满分: 9分
填空1: (3分)
n==0
或者:0==n
填空2: (6分)
f(n-i*i, a, idx+1)
或者:
f(n-i*i, a, idx+1) > 0
f(n-i*i, a, idx+1) == 1
试题2
在对文本进行简单加密的时候,可以选择用一个n位的二进制数,对原文进行异或运算。 解密的方法就是再执行一次同样的操作。 加密过程中n位二进制数会循环使用。并且其长度也可能不是8的整数倍。 下面的代码演示了如何实现该功能。 请仔细阅读,填写空缺的代码(下划线部分)。 void f(char* buf, unsigned char* uckey, int n) { int i; for(i=0; i<n; i++) buf[i] = buf[i] ^ uckey[i]; //异或运算,即:buf[i] ^= uckey[i] } int main(int argc, char* argv[]) { char p[] = "abcd中国人123"; // 待加密串 char* key = "11001100010001110"; //以串的形式表达的密匙,运算时要转换为按位存储的形式。 int np = strlen(p); int nk = strlen(key); unsigned char* uckey = (unsigned char*)malloc(np); // unsigned char是无符号字节型,char类型变量的大小通常为1个字节(1字节=8个位) // 密匙串需要按位的形式循环拼入 uckey中 int i; for(i=0; i<np*8; i++) { if(key[i%nk]=='1') ______; // 填空1按位或 else ______; // 填空2按位与 } f(p, uckey, strlen(p)); f(p, uckey, strlen(p)); printf("%s ", p); free(uckey); return 0; } uckey[i/8] |= (unsigned char)0x80 >> (i%8) uckey[i/8] &= ~((unsigned char)0x80 >> (i%8))
本题满分:14分
填空1:(7分)
uckey[i/8] |= (unsigned char)0x80 >> (i%8); //>>表示右移位,位逻辑运算符:&按位与,|按位或,^按位异或,~取反,移位运算符:<<左移,>>右移
从数学上看,左移1位等于乘以2,右移1位等于除以2,然后再取整,移位溢出的丢弃
填空2:(7分)
uckey[i/8] &= ~((unsigned char)0x80 >> (i%8));
注意所有逻辑等价形式都是正确的答案,比如可以使用左移位:
(unsigned char)0x80 >> 2 等价于:0x01 << 5
试题3
为什么1小时有60分钟,而不是100分钟呢?这是历史上的习惯导致。 但也并非纯粹的偶然:60是个优秀的数字,它的因子比较多。 事实上,它是1至6的每个数字的倍数。即1,2,3,4,5,6都是可以除尽60。 我们希望寻找到能除尽1至n的的每个数字的最小整数。 不要小看这个数字,它可能十分大,比如n=100, 则该数为: 69720375229712477164533808935312303556800 请编写程序,实现对用户输入的 n (n<100)求出1~n的最小公倍数。 例如: 用户输入: 6 程序输出: 60 用户输入: 10 程序输出: 2520 要求考生把所有函数写在一个文件中。调试好后,存入与考生文件夹下对应题号的“解答.txt”中即可。 相关的工程文件不要拷入。 对于编程题目,要求选手给出的解答完全符合ANSI C标准,不能使用c++特性; 不能使用诸如绘图、中断调用等硬件相关或操作系统相关的API。
import java.math.BigInteger; import java.util.Scanner; public class Main { public void getResult(int n) { BigInteger temp1 = BigInteger.ONE; BigInteger temp2 = BigInteger.ONE; BigInteger temp3 = BigInteger.ONE; for(int i = 2;i <= n;i++) { temp1 = temp3; temp2 = new BigInteger(""+i); temp3 = temp1.gcd(temp2); temp3 = temp1.multiply(temp2).divide(temp3); } System.out.println(temp3); } public static void main(String[] args) { Main test = new Main(); Scanner in = new Scanner(System.in); int n = in.nextInt(); test.getResult(n); } }
来自网友C语言版:
解答: 最小公倍数就是所有质数的相应幂的积 比如N=10 小于10的质数有2,3,5,7 对应的最大幂是:3,2,1,1 则最小公倍数是:2^3x3^2x5^1x7^1 = 2520 #include <iostream> #include <cstring> #include <cmath> using namespace std; int a[50] = {0};//存素数 bool vis[100]; int b[50] = {0};//存幂次 void init_prim()//求小于100的所有素数存入数组a { int i,j,k; int m = (int)(sqrt(100.0)+0.5); memset(vis,0,sizeof(vis)); vis[0] = 1; vis[1] = 1;//必须加上,否则第一个素数别认为是1 for(i=2; i<=m; i++) if(!vis[i]) { for(j=2*i; j<=100; j+=i) vis[j] = 1; } int t = 0; for(k=0; k<100; k++) if(!vis[k]) a[t++] = k; } int main() { int i,j,k; init_prim(); int n; //2^6 = 64,2^7 = 128;由于n最大100,幂次最大6 // for(i=0 ; i<100; i++)//素数没问题 // if(!vis[i]) // cout<<i<<endl; // while(1); while(cin>>n) { memset(b,0,sizeof(b)); for(i=0; i<=n&&a[i]<=n; i++)//”1到n素数个数小于n的一半 “不对,3有两个素数 { // cout<<a[i]<<"-----"<<endl; for(j=1; j<=6; j++) { if(pow((double)a[i],(double)j)>(double)n) { b[i] = j -1;//b的下标不必新开 break; } else if(pow((double)a[i],(double)j) == (double)n)//必须分开 { b[i] = j; break; } } } //不知道是不是pow函数的问题,把ans定义为int得出的结果出问题,double就对了 double ans = 1; for(k=0; k<i; k++) { //cout<<a[k]<<"........"<<b[k]<<endl; ans *= pow((double)a[k],(double)b[k]); } cout<<(int)ans<<endl; } return 0; } //该程序 到25时就溢出,ans换位long long前几个就错误啦,此时需要把pow函数换掉 #include <iostream> #include <cstdio> #include <cstring> #include <cmath> using namespace std; const int N = 105; int n; int a[N][50]; int b[N] = {0}; void multiply() { int i,j,k; memset(a,0,sizeof(a)); for(i=3; i<=100; i++) { /* 下面的是直接按平常的乘法,乘数的一位乘以被乘数的每一位并处理进位;另外是乘数整体乘以被乘数的每一位最后统一处理进位 */ int temp = 0; a[i][0] = 1;//很重要 for(j=2; j<=i; j++) { int c = 0; for(k=0; k<50; k++)//最大不超过160位 ,目前是100!,最后除以3等50 { temp = a[i][k]*b[j] + c; a[i][k] = temp%1000; c = temp/1000; } } } } void printData(int n) { int i,j,k; for(i=49; i>=0; i--) if(a[n][i]) break; cout<<a[n][i];//第一个不输出前导0 for(j=i-1; j>=0; j--) printf("%03d",a[n][j]); cout<<endl; } int main() { int i, j, k; for(i=0; i<N; i++) b[i] = i; for(i=2; i<N; i++) for(j=i+1; j<=N; j++) { if(b[j]%b[i]==0) b[j] /= b[i]; //cout<<b[j]<<endl; } //for(i=0; i<100; i++) // cout<<b[i]<<endl; //while(1); multiply(); while(cin>>n) { if(n==1||n==2) { cout<<n<<endl; continue; } printData(n); } return 0; }
试题4
为解决交通难题,某城市修建了若干条交错的地铁线路,线路名及其所属站名如stations.txt所示。 线1 苹果园 .... 四惠东 线2 西直门 车公庄 .... 建国门 线4 .... 其中第一行数据为地铁线名,接下来是该线的站名。 当遇到空行时,本线路站名结束。 下一行开始又是一条新线....直到数据结束。 如果多条线拥有同一个站名,表明:这些线间可以在该站换车。 为引导旅客合理利用线路资源,解决交通瓶颈问题,该城市制定了票价策略: 1. 每条线路可以单独购票,票价不等。 2. 允许购买某些两条可换乘的线路的联票。联票价格低于分别购票。 单线票价和联合票价如 price.txt 所示。 线1 180 ..... 线13 114 线1,线2 350 线1,线10 390 ..... 每行数据表示一种票价 线名与票价间用空格分开。如果是联票,线名间用逗号分开。 联票只能包含两条可换乘的线路。 现在的问题是:根据这些已知的数据,计算从A站到B站最小花费和可行的换乘方案。 比如,对于本题目给出的示例数据 如果用户输入: 五棵松,奥体中心 程序应该输出: -(线1,线10)-线8 = 565 如果用户输入: 五棵松,霍营 程序应该输出: -线1-(线4,线13) = 440 可以看出,用户输入的数据是:起始站,终到站,用逗号分开。 程序输出了购票方案,在括号中的表示联票,短横线(-)用来分开乘车次序。 等号后输出的是该方案的花费数值。 请编程解决上述问题。 注意: 1. 我们测试您的程序时,所用数据与题目中的示例数据不同,但格式完全一样。 2. 当多个方案有相同的最小花费,输出任意一个方案即可。 要求考生把所有类写在一个文件中。 调试好后,存入与考生文件夹下对应题号的“解答.txt”中即可。 相关的工程文件不要拷入。请不要使用package语句。
对于此题,重点在于文本文件中信息的读取,并选择合适的数据结构来处理分类,好复杂的感觉,又看到相关备注,说明:此题类型在第四届以后便不再用这种形式来出题,所以就简单的看了一下网友的代码,没有自己上机实现。
Java版:蓝桥杯-地铁换乘
来自网友的C语言版:
1 #include<iostream> 2 using namespace std; 3 #define LEN 50 4 typedef struct stations{ 5 char name[20]; 6 int len; 7 int roads[50]; 8 struct stations *left; 9 struct stations *right; 10 }Stations; 11 12 typedef struct etree{ 13 int value; 14 int roadNum; 15 struct etree *father; 16 int childnum; 17 }ETree; 18 19 typedef struct queue{ 20 ETree *tie; 21 struct queue *next; 22 }Queue; 23 24 void pushQueue(Queue &head, ETree *&etree){ 25 Queue *p=head.next,*q=&head; 26 while(p!=NULL && (p->tie->value<etree->value)){ 27 q=p; 28 p=p->next; 29 } 30 q->next=(Queue*)malloc(sizeof(Queue)); 31 q->next->tie=etree; 32 q->next->next=p; 33 } 34 void freeEtree(ETree *q){ 35 ETree *p; 36 while(q->childnum==0){ 37 p=q; 38 q=q->father; 39 free(p); 40 if(q!=NULL) 41 q->childnum--; 42 else 43 break; 44 } 45 } 46 47 void freeAll(Stations *&head){ 48 if (head!=NULL){ 49 freeAll(head->left); 50 freeAll(head->right); 51 free(head); 52 } 53 } 54 55 void showBest(ETree *h,int price[][LEN],char roadName[][20],int roadNum){ 56 if(h!=NULL){ 57 if (h->faher==NULL){ 58 printf("%s",roadName[h->roadNum]); 59 } 60 else{ 61 int j; 62 j=h->roadNum; 63 if (h->value==(price[j][j]+h->father->value)){ 64 showBest(h->father,price,roadName,roadNum); 65 if (price[j][roadNum]){ 66 printf("-(%s,%s)",roadName[j],roadName[price[j][roadNum]-1]); 67 68 } 69 else 70 printf("-%s",roadName[j]); 71 } 72 else{ 73 showBest(h->father->father,price,roadNme,roadNum); 74 printf("-(%s,%s)",roadName[h->father->roadNum],roadName[j]); 75 } 76 } 77 } 78 } 79 80 inline int compares(char s1[],int n1,chr s2[],int n2){ 81 if (n1!=n2) 82 return n1-n2; 83 return strcmp(s1,s2); 84 } 85 boll findStation(Stations* &head,Stations* &p,char s[]){ 86 int len=strlen(s); 87 int t; 88 Stations q; 89 p=head; 90 while (n!=NULL){ 91 q=p; 92 t=compares(s,len,p->name,p->len); 93 if (t<0) 94 p=p->left; 95 else 96 retrn true; 97 } 98 p=q; 99 return false; 100 } 101 102 void insert(Stations* &head,char s[],int road,int price[][LEN]{ 103 Stations *p,*q; 104 int t; 105 t=strlen(s); 106 if(s[t-1]==' ') 107 s[t-1]='�'; 108 if(head==NULL){ 109 p=(Stations *)malloc(sizeof(Stations)); 110 p->left=NULL; 111 p->rght=NULL; 112 strcpy(p->name,s); 113 p->len=strlen(s); 114 p->road[0]=1; 115 p->road[1]read; 116 head=p; 117 } 118 else{ 119 if (findStation(head,p,s)){ 120 p->roads[0]++; 121 t=p->roads[0]; 122 p->roads[t]=road; 123 for(t--;t>0,t--){ 124 price[p->road[t]][road]=-1; 125 price[road][p->road[t]]=-1; 126 } 127 } 128 else{ 129 q=p; 130 p=(Stations *)malloc(sizeof(Stations)); 131 p->left=NULL; 132 p->right=NULL; 133 strcpy(p->name,s); 134 p->len=strlen(s); 135 p->road[0]=1; 136 p->road[1]=road; 137 t=compares(s,p->len,q->name,q->len); 138 if(t<0) 139 q->left=p; 140 else 141 q->right=p; 142 } 143 } 144 } 145 146 int GetRoadNum(char *r,char roadName[][20],int road Num){ 147 for (int i=0;i<roadNum;i++) 148 if (strcmp(roadName[i],r)==0) 149 return i; 150 return 0; 151 } 152 153 void main() 154 { 155 //[roadnum][roadnum+1] 156 int price[LEN][LEN]={0}; 157 char roadName[LEN][20]; 158 int i,j,k,t; 159 char line[20]; 160 int roadNum; 161 Stations *head=NULL; 162 FILE *fp; 163 if((fp=fopen("stations.xt","r"))==NULL){ 164 printf("找不到stations文件 "); 165 return; 166 } 167 roadNum=0; 168 while(!feof(fp)){ 169 fscanf(fp,"%s%*c",roadName[roadNum]); 170 fgets(line,19,fp); 171 while(!feof(fp)&&line[0]!=' '){ 172 insert(head,line,roadNum,price); 173 fgets(line,19,fp); 174 } 175 roadNum++; 176 } 177 roadNum++; 178 } 179 insert(head,line,roadNum-1,price); 180 fclose(fp); 181 if ((fp=fopen("price.txt","r"))==NULL){ 182 printf("找不到price文件"); 183 } 184 while (!feof(fp)){ 185 fscanf(fp,"%s,line); 186 fscanf(fp,"%d",&k); 187 for(t=0;line[t]!='�'&&line[t]!=",";t++); 188 if (line[t]==','){ 189 line[t]='�'; 190 i=GetRoadNum(line,roadName,roadNum); 191 j=GetRoadNum(line+t+1,roadName,roadNm); 192 price[i][j]=k; 193 price[j][i]=k; 194 if (price[i][i]>k){ 195 price[i][roadNum]=j+1; 196 } 197 if (price[j][j]>k){ 198 price[j][j]=k; 199 price[j]roadNum]=i+1; 200 } 201 } 202 else{ 203 i=GetRoadNum(line,roadName,roadNum); 204 price[i][i]=k; 205 } 206 } 207 208 fclose(fp); 209 210 char starts[20]={"五棵松"},ends[20]="奥体中心"}; 211 Stations *sroad,*eroad; 212 Queue Qhead, *h; 213 Etree *p,*q; 214 while(true){ 215 char Flag[LEN]={0};//为-1表示目标,为0表示尚未发生过扩展 216 Qhead.next=NULL; 217 Qhead.tie=NULL; 218 scanf("%[^, ]s",starts); 219 if (getchar()!=',') 220 break; 221 scanf("%[^ ]s",ends); 222 getchar(); 223 if (!findStation(head,sroad,starts)){ 224 printf("未找到%s的匹配项 ",starts); 225 continue; 226 } 227 if (!findStation(head,eroad,ends)){ 228 printf("未找到%s的匹配项 ",ends); 229 continue; 230 } 231 for (i=1;i<=sroad->roads[0];i++){ 232 p=(ETree*)malloc(sizeof(ETree)); 233 p->father=NULL; 234 p->childnum=0; 235 p->roadNum=sroad->roads[i]; 236 p->value=price[p->roadum][p->roadNum]; 237 pushQueue(Qhead,p); 238 } 239 for (i=1;i<=eroad->roads[0];i++){ 240 Flag[eroad->roads[i]]=-1; 241 } 242 while(Qhead.next!=NULL){ 243 h=Qhead.next; 244 q=h->tie; 245 if (Flag[q->roadNum]==-1){ 246 break; 247 } 248 Qhuad.next=Qhead.next->next; 249 i=q->roadNum; 250 if (Flag[i]!=1){ 251 for(j=0;j<roadNum;j++){ 252 if (price[i][j]){ 253 q->childnum++; 254 p=(ETree*)malloc(sizeof(ETree)); 255 p->father=q; 256 p->childnum=0; 257 p->roadNum=j; 258 k=price[j][j]>0){ 259 if(price[i][j]>0){ 260 if(q->father!=NULL) 261 t=price[i][j]+q->father->value; 262 else 263 t=price[i][j]; 264 if (k>t) 265 k=t; 266 } 267 p->value=k; 268 pushQueue(Qhead,p); 269 } 270 } 271 Flag[i]=1; 272 } 273 freeETree(h->tie); 274 free(h); 275 } 276 if (Qhead.next!=NULL){ 277 showBest(q,price,roadName,roadNum); 278 printf("=%d ",q->value); 279 } 280 else 281 printf("此路不通 "); 282 for(;Qhead.next!=NULL;){ 283 h=Qead.next; 284 Qhead.nexQhead.next->next; 285 freeETree(h->tie); 286 free(h); 287 } 288 } 289 freeAll(head); 290 }
试题5
BMP是常见的图像存储格式。 如果用来存黑白图像(颜色深度=1),则其信息比较容易读取。 与之相关的数据: (以下偏移均是从文件头开始) 偏移:10字节, 长度4字节: 图像数据真正开始的位置。 偏移:18字节, 长度4字节: 位图的宽度,单位是像素。 偏移:22字节, 长度4字节: 位图的高度,单位是像素。 从图像数据开始处,每个像素用1个二进制位表示。 从图片的底行开始,一行一行向上存储。 Windows规定图像文件中一个扫描行所占的字节数必须是4字节的倍数, 不足的位均以 0 填充。例如,图片宽度为45像素,实际上每行会占用 8个字节。 可以通过Windows自带的画图工具生成和编辑二进制图像。 需要在“属性”中选择“黑白”,指定为二值图像。 可能需要通过 查看 | 缩放 | 自定义... 把图像变大比例一些, 更易于操作。 图像的左下角为图像数据的开始位置。白色对应1,黑色对应0 我们可以定义:两个点距离如果小于2个像素,则认为这两个点连通。 也就是说:以一个点为中心的九宫格中,围绕它的8个点与它都是连通的。 如:t1.bmp 所示,左下角的点组成一个连通的群体; 而右上角的点都是孤立的。 in.bmp t1.bmp 程序的目标是:根据给定的黑白位图,分析出所有独立连通的群体, 输出每个连通群体的面积。所谓面积,就是它含有的像素的个数。 输入数据固定存在in.bmp中。 如示例的in.bmp, 程序应该输出: 12 81 52 133 该输出表示:共有4个连通群体。 输出的连通体面积间的顺序可以随意。 请编程解决上述问题。 我们测试程序的时候,会使用不同的in.bmp文件。 要求考生把所有类写在一个文件中。 调试好后,存入与考生文件夹下对应题号的“解答.txt”中即可。 相关的工程文件不要拷入。请不要使用package语句。
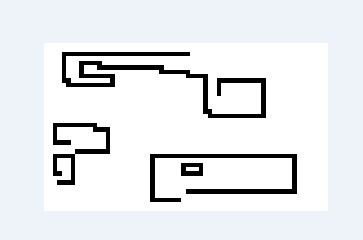
图 in.bmp

图 t1.bmp
这题要读入图片文件数据,感觉头大啊,此前做的题,几乎没有遇到要读取文件中的数据,而现在竟然还碰到了读取图片的数据,看到此题的核心:即使用DFS求取连通图的问题,并且返回每一个连通图中包含的顶点个数,但是对于此题处理读取数据的问题,就没有仔细去探究,下面贴出一段网友的C语言代码,以作参考:
1 include<stdio.h> 2 #include<stdlib.h> 3 #include<malloc.h> 4 #include<string.h> 5 6 void main(){ 7 int i,j,k,m; 8 int width,height,start,world; 9 int *bmp,*Lcount; 10 bool *Lflag; 11 FILE *fp; 12 if((fp=fopen("in1.bmp","rb"))==NULL){ 13 printf("文件打开失败"); 14 return; 15 } 16 fseek(fp,10L,0); 17 fscanf(fp,"%4c",&start); // 4c表示该数据占4个字节 18 // printf("start = %d ",start); 19 fseek(fp,18,0); 20 fscanf(fp,"%4c",&width); 21 // printf("width = %d ",width); 22 fseek(fp,22,0); 23 fscanf(fp,"%4c",&height); 24 // printf("height = %d ",height); 25 bmp = (int*)malloc((width+2)*sizeof(int)); 26 memset(bmp,0,(width+2)*sizeof(int)); 27 Lcount = (int*)malloc(width*sizeof(int)); 28 memset(Lcount,0,width*sizeof(int)); 29 Lflag = (bool*)malloc(width*sizeof(bool)); 30 memset(Lflag,0,width*sizeof(bool)); 31 Lcount--; 32 Lflag--; 33 fseek(fp,start,0); 34 world = ( width%32 ? width/32+1 : width/32 )*4; 35 int last,i1,i2,i3; 36 int eCount = 0 37 for(i=0 i<height i++ ){ 38 char c; 39 k=1; 40 last=0; 41 for(j=0 j<world j++){ 42 fscanf(fp,"%c",&c); 43 for(m = 7 m >= 0 && k<=width m-- ){ 44 if( !( 1<<m & c ) ){ 45 //printf("*"); 46 if(bmp[k]){ 47 last = bmp[k]; 48 Lcount[last]++; 49 Lflag[last] = true 50 } 51 else{ 52 i1 = last ? last : bmp[k-1] 53 i3 = bmp[k+1] 54 last = 0; 55 if( i1 || i3){ 56 if( i1 && i3 && ( i1 != i3 ) ){//确定需要连接 57 Lcount[i1] += Lcount[i3] 58 Lcount[i3]=0; 59 for(i2=1;i2<=width i2++){ 60 if(bmp[i2]==i3) 61 bmp[i2] = i1; 62 } 63 } 64 else{ 65 if(!i1) 66 i1=i3; 67 } 68 bmp[k] = i1 69 Lcount[i1]++; 70 Lflag[i1] = true 71 } 72 else{//插入 73 for(i2=1;Lcount[i2];i2++); 74 Lcount[i2]=1; 75 bmp[k] = i2 76 Lflag[i2] = true 77 } 78 } 79 } 80 else{ //printf(" "); 81 last = bmp[k] 82 bmp[k] = 0 83 } 84 k++; 85 } 86 } 87 //printf(" "); 88 for(i2=1;i2<=width;i2++){ 89 if(Lcount[i2] && !Lflag[i2] ){ 90 printf("%d ",Lcount[i2]); 91 Lcount[i2] = 0 92 eCount++; 93 } 94 Lflag[i2]=false; 95 } 96 } 97 fclose(fp); 98 free(Lflag+1); 99 free(Lcount+1); 100 free(bmp); 101 printf("count=%d ",eCount); 102 }