英文原文请参考http://www.deeplearning.net/tutorial/rbm.html
能量模型
Energy-based models associate a scalar energy to each configuration of the variables of interest.学习并修改相应的能量函数使得shape有较好的属性。基于能量的概率模型通过能量函数定义一个概率分布，如下：
归一化因子Z被叫做配分函数，类比于物理系统。
基于能量的模型可以通过对训练数据的负似然函数执行梯度下降来进行学习。如下：类似于逻辑回归，先定义似然函数，损失函数为负值。
使用随机梯度
，
是模型的参数。
带隐藏层的能量模型
In many cases of interest, we do not observe the example 
fully, or we want to introduce some non-observed variables to increase the expressive power of the model.（类似于dA）。因此我们考虑可观察部分x和隐藏部分h，重定义概率分布，如下：
（2）
为了与前面的公式类似，我们引进自由能(free energy)，定义如下：
有，
梯度有了新的形式：
（4）
上述梯度包含两个terms，positive and negative phase，反映模型的概率密度。第一个term增加训练数据的概率（通过减少相应的能量）,第二个term则降低样本的概率。
通常很难确定这个梯度，因为它包含
的计算。 This is nothing less than an expectation over all possible configurations of the input (under the distribution 
formed by the model) !
使得该计算tractable的第一步是使用固定数量的模型样本来估计期望。用于估计负梯度的样本叫做negative particles，记为
。梯度可以表示为下：
（5）
通过上面公式我们几乎获得一个实用的随机的算法去学习EBM，唯一缺少的就是如何去抽取。Markov Chain Monte Carlo 方法尤其适合RBM这样的模型，一种特殊的EBM。
Restricted Boltzmann Macheines ,RBM
RMB是log-linear Markov Random Field的特殊形式，其能量函数是线性的。为了有效表示复杂的分布（从限制的参数设置到无参），我们考虑一些变量永不可观察（即隐藏），更多的隐藏变量可以增加波兹曼机BM的modeling capacity。RBM就是进一步限制visible-visible和hidden-hidden的连接，图形表示如下：
能量函数定义为：
（6）
其中W表示连接可见单元和隐藏单元的权重，b,c分别代表可见层和隐藏层的偏移量offsets。
转换成自由能公式：
由于RBM的特殊结构，可见和隐藏单元是条件依赖的，如下：
RBMs with binary units
一般研究中使用二进制单元 
，通常的神经元激活函数的概率如下：
二进制单元的RMB自由能简化如下：
（9）
结合公式（5）和（9），我们获得以下负似然梯度：
详细的公式推到请参考以下文章page，Learning Deep Architectures for AI.然而我们并不使用这些公式，而是通过Theano的T.grad获得梯度。
采样
通过运行Markov链到收敛来获得p(x)的样本，使用Gibbs采样作为转移操作。
N个随机变量的Gibbs采样is done through a sequence of N sampling sub-steps of the form 
where 
contains the 
other random variables in 
excluding 
.
对于RBM，S包含可见和隐藏单元的集合。它们之间是条件依赖的，因此给定一个，另一个同时被采样，在马尔科夫链中的一步表示如下：
以
的概率随机取0或1，同样地，
以
的概率随机取0或1。图形表示如下：
As 
, samples 
are guaranteed to be accurate samples of 
.
理论上，学习过程中的每次参数更新需要在这样的链上跑一遍直至收敛。耗费巨大，因此，一些算法被设计，为了在学习过程中有效地从p(v,h)取样。
对比散度Contrastive Divergence (CD-k)
对比差异使用两种技巧加速采样过程：
- 因为我们最终想要
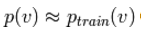，我们用训练样本初始化马尔可夫链（如期待接近于p的分布，以致于可以很快地收敛到最终的分布）。 - CD并不直到链收敛。通过仅仅k步Gibbs采样获得样本。在实际中，k=1就已经表现出很好的效果。
持续化CD
持续CD使用另一种近似方法从p(v,h)采样。它依赖于单一的Markov链，有一个持久的状态（i.e., not restarting a chain for each observed example）。对每次的参数更新，通过仅仅运行k步chain来抽取新的样本。为后续更新保存链路状态。
The general intuition is that if parameter updates are small enough compared to the mixing rate of the chain, the Markov chain should be able to “catch up” to changes in the model.
代码实现部分请参考下一篇博文：Deep Learning Tutorial (翻译) 之 RBM（下）
More 参考资料：