1.最大子段和问题的描述

2.分治策略的求解思路
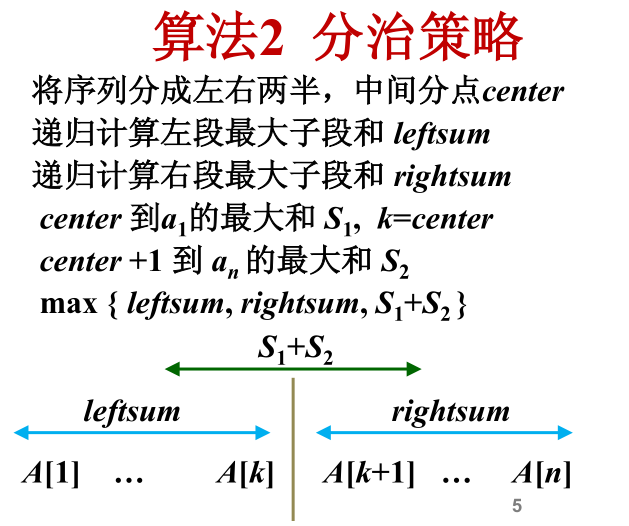
用分治法求解这个问题 。
在数组的 center = (right-left)/2+left 位置处分开。形成两个子数组。
那么,最大子段和 可能出现在三个位置:
a.可能出现在 左 子数组
b. 可能出现在 右子数组
c.可能出现在 过center的 中间某部分 元素 组成的子数组。
(一定会过center 吗? 为什么一定会过center?因为这是分治过程,center的值会发生改变,当然,计算中所包含的数也会发生改变,所以,不要死盯着 (0+array.length)/2 的center,center 是 (left+right)/2 ,而不是 (0+array.length)/2
下面考虑 三种情况的计算方法:
第一种情况: 计算 left 到 center 的最大和,记作 leftSum
第二种情况: 计算从 center+1 到 right的最大和,记作 rightSum
第三种情况: 跨边界的和。 ;以center为中心分别向两边计算和。
a.从 center出发,每次向左边扩张一步,并且记录当前的值S1,如果当前的和比上次的和大,就更新S1,一 直向左扩张到 位置 Left。
b.从 center+1出发,每次扩张一步,计算当前的和 为S2,如果当前的值比上次的和 大,那么,就更新S2的 值,一直向右扩张到位置Right。
c.计算过center的连续值的和,S1+S2的值 Sum。 这个就是跨边界的和。
上面三种情况考虑计算完成后,最后一步就是,比较三个值中的最大值,取最大值就可以了。
3.分治方法求解的伪码

4.最后考虑用分治方法求解的时间复杂度。
我们在(left+right)/2处,把大问题分成了两个部分的小问题
T(N)1=2T(N) , T(N)2=N
在跨边界求和的时候,我们需要计算 从center出发的到 left方向的最大和,每次增加一个元素,通过比较,得到最大的和,
时间复杂度为O(N),同样, 从center+1 出发的到 right 方向的最大和,每次增加一个元素,通过比较,得到最大的和,时间复杂度 为 O(N) ,所以,时间复杂度为 O(N)

5. 代码