题目
标题:二阶魔方
魔方可以对它的6个面自由旋转。
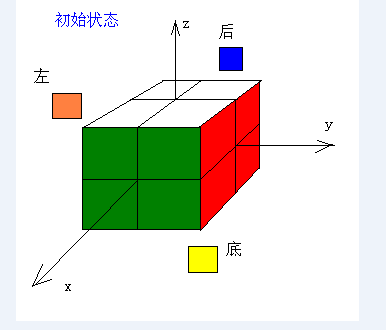
我们来操作一个2阶魔方(如图1所示)
为了描述方便,我们为它建立了坐标系。
各个面的初始状态如下:
x轴正向:绿
x轴反向:蓝
y轴正向:红
y轴反向:橙
z轴正向:白
z轴反向:黄
假设我们规定,只能对该魔方进行3种操作。分别标记为:
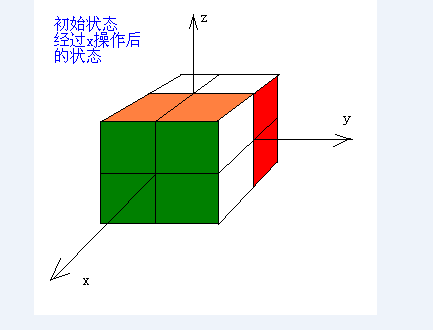
x 表示在x轴正向做顺时针旋转
y 表示在y轴正向做顺时针旋转
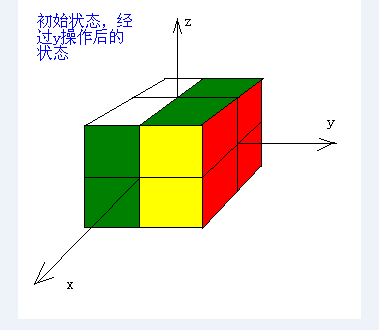
z 表示在z轴正向做顺时针旋转
基本旋转后的效果如图2,3,4所示。
xyz 则表示顺序执行x,y,z 3个操作
题目的要求是:
从标准输入获得一个串,表示操作序列。
程序输出:距离我们最近的那个小方块的3个面的颜色。
顺序是:x面,y面,z面。
例如:在初始状态,应该输出:
绿红白
初始状态下,如果用户输入:
x
则应该输出:
绿白橙
初始状态下,如果用户输入:
zyx
则应该输出:
红白绿
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。

package com.lanqiaobei.moni;
import java.util.Scanner;
import java.util.StringTokenizer;
public class Main {
//定义24个面的颜色
public String[] mian=new String[25];
public static void main(String[] args) {
// TODO Auto-generated method stub
Main m=new Main();
m.init();
m.getString();
m.getResult();
}
//定义读取函数
public void getString(){
Scanner sc=new Scanner(System.in);
String str=sc.nextLine();
for (int i=0;i<str.length();i++){
String next=str.substring(i, i+1);
if (next=="x"){
reX();
}
if (next=="y"){
reY();
}
if (next=="z"){
reZ();
}
}
}
//初始化24个面的颜色
public void init(){
for (int i=1;i<5;i++){ //x zheng
mian[i]="绿";
}
for (int i=5;i<9;i++){ //y zheng
mian[i]="红";
}
for (int i=9;i<13;i++){ //z zheng
mian[i]="白";
}
for (int i=13;i<17;i++){ //x fan
mian[i]="蓝";
}
for (int i=17;i<21;i++){ //y fan
mian[i]="橙";
}
for (int i=21;i<25;i++){ //z fan
mian[i]="黄";
}
}
//输出结果(最靠近我们那个正方体的三个面)
public void getResult(){
System.out.println(mian[2]+mian[5]+mian[9]);
}
//定义绕x轴旋转的函数
public void reX(){
String[] sa=revertZheng(mian[1],mian[2],mian[3],mian[4]);
for(int i=1;i<5;i++){
mian[i]=sa[i-1];
}
String[] sb=revertZheng(mian[10],mian[9],mian[5],mian[8],mian[22],mian[21],mian[19],mian[18]);
mian[10]=sb[0];mian[9]=sb[1];mian[5]=sb[2];mian[8]=sb[3];
mian[22]=sb[4];mian[21]=sb[5];mian[19]=sb[6];mian[18]=sb[7];
}
//定义绕y轴旋转的函数
public void reY(){
String[] sa=revertZheng(mian[5],mian[6],mian[7],mian[8]);
mian[5]=sa[0];mian[6]=sa[1];mian[7]=sa[2];mian[8]=sa[3];
String[] sb=revertZheng(mian[9],mian[12],mian[13],mian[16],mian[23],mian[22],mian[3],mian[2]);
mian[9]=sb[0];mian[12]=sb[1];mian[13]=sb[2];mian[16]=sb[3];
mian[23]=sb[4];mian[22]=sb[5];mian[3]=sb[6];mian[2]=sb[7];
}
//定义绕z轴旋转的函数
public void reZ(){
String[] sa=revertZheng(mian[10],mian[11],mian[12],mian[9]);
mian[10]=sa[0];mian[11]=sa[1];mian[12]=sa[2];mian[9]=sa[3];
String[] sb=revertZheng(mian[18],mian[17],mian[14],mian[13],mian[6],mian[5],mian[2],mian[1]);
mian[18]=sb[0];mian[17]=sb[1];mian[14]=sb[2];mian[13]=sb[3];
mian[6]=sb[4];mian[5]=sb[5];mian[2]=sb[6];mian[1]=sb[7];
}
//定义正对我们那四个面的旋转函数
public String [] revertZheng(String s1,String s2,String s3,String s4){
String a="";
a=s1;
s1=s4;
s4=s3;
s3=s2;
s2=a;
String[] ss=new String[4];
ss[0]=s1;ss[1]=s2;ss[2]=s3;ss[3]=s4;
return ss;
}
//侧面8个面的旋转函数
public String [] revertZheng(String s1,String s2,String s3,String s4,String s5,String s6,String s7,String s8){
String a="",b="";
a=s1;b=s2;
s1=s7;
s2=s8;
s7=s5;
s8=s6;
s5=s3;
s6=s4;
s3=a;
s4=b;
String[] ss=new String[8];
ss[0]=s1;ss[1]=s2;ss[2]=s3;ss[3]=s4;ss[4]=s5;ss[5]=s6;ss[6]=s7;ss[7]=s8;
return ss;
}
}