模拟退火算法学习笔记

摘自：百度百科，《算法竞赛入门到进阶》

一：概念

是一种基于概率的算法

它是基于Monte-Carlo迭代求解策略的一种随机寻优算法

结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。

理论上算法具有概率的全局优化性能

二：基于的物理原理：

一个高温物体降温到常温，温度越高时，降温的概率越大(更快)，温度越低时降温的概率越小(更慢)。模拟退火算法就是利用这样的思想进行搜索，多次降温(迭代)，直到获得一个可行解。

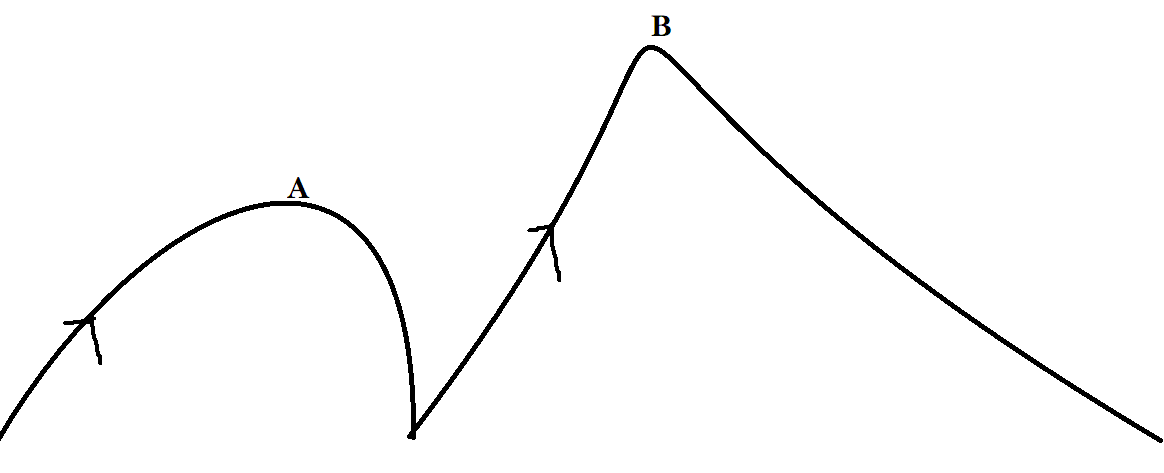
如图，A是局部最高点，B是全局最高点。普通贪心，如果在A附近，会停在局部最高点A，无法到达B。但模拟退火算法可以跳出A，得到B。它可以以一定的概率来接受比当前点更低的点，使程序有机会摆脱局部最优到达全局最优，这个概率会随时间不断减小，从而最后能限制在最优解附近。

三：主要步骤

(1)设置一个初始温度T

(2)温度下降，状态转移。从当前温度按降温系数下降到下一个温度，在新的温度计算当前状态。

(3)如果温度降到设定的温度下界，程序停止

伪代码：

    eps=1e-8;    //终止温度，接近0，用于控制精度 
    T=100;        //初始温度，应该是高温，100°为例 
    delta=0.98;    //降温系数，控制退火的快慢，小于1，以0.98为例
    g(x)        //状态x的评价函数，例如能量
    now,next;    //当前状态和新状态
    while(T>eps)    //如果当前温度未降到eps 
    {
        g(next),g(now);    //计算能量 
        dE=g(next)-g(now);    //能量差 
        if(dE>=0)        // 新状态更优，接受 
            now=next;     
        else if(exp(dE/T)>rand())    //如果新状态更差，在一定概率下接受它，e^(dE/T) 
            now=next;
        T*=delta;    //降温，模拟退火过程 
    } 

科学家理论分析，概率为：e^(dE/T)

四：参数

模拟退火在调参方面比较麻烦，参数要合适才能得到比较优的解，因为初学，经验不足，先留个坑吧。

五：应用

HDU 2899　　求函数最小值