一:
定义:
对正整数n,欧拉函数是小于或等于n的正整数中与n互质的数的数目(φ(1)=1)
比如对于φ(6)来讲,1,2,3,4,5,6,为1,5。所以φ(6)=2。
二:
公式:
首先是分解质因子。
随后是:
![]()
三:
部分性质:
1:当n为奇质数时,φ(2n)=φ(n)
2:当n为质数时,φ(n)=n-1;
四:
求欧拉函数
1:直接根据公式求欧拉函数
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int maxn=1e5+50; const int mod=1e9+7; const int inf=1e9; //int gcd(int a,int b) //{ // return b?gac(b,a%b):a; //} int main() { // map<int,int>mp; int n; cin>>n; while(n--) { ll x; cin>>x; ll sum=x; for(int i=2;i<=x/i;i++) { if(x%i==0) { sum=sum/i*(i-1); while(x%i==0) { // mp[i]++; x=x/i; } } } if(x>1) sum=sum/x*(x-1); cout<<sum<<endl; } }
2:筛法求欧拉函数
phi表示φ(欧拉函数值)
(1)(i%pr[j]==0
由之前的埃氏筛法,if(i%pr[j]==0)。那么pr[j]为i的最小质因子。
所以φ(i*pr[j])=pr[j]*φ(i)
所以有:
if(i%prime[j]==0) { phi[prime[j]*i]=phi[i]*prime[j]; break; }
(2)(i%pr[j]!=0
首先对于i,假设其质因子为p1~pk,则其欧拉函数φ(i)==i*(1-1/p1)*....(1-1/pk)
i*pr[j]的质因子,包括p1~pk,再加个pr[j]。那么其欧拉函数:
φ(pr[j]*i)
==pr[j]*i*(1-1/p1)*....(1-1/pk)*(1-1/pr[j])
==φ(i)*pr[j]*(1-1/pr[j])
==φ(i)*(pr[j]-1)
那么有:
phi[prime[j]*i]=phi[i]*(prime[j]-1);
可以看到,此式与(1)的区别仅为prime[j]是否-1而已。
板子:
int prime[maxn]; int tot=0; int phi[maxn];//欧拉 bool st[maxn]; ll get_phi(int n) { phi[1]=1; for(int i=2;i<=n;i++) { if(!st[i]) { prime[tot++]=i; phi[i]=i-1;//1~i-1均与i互质 } for(int j=0;prime[j]<=n/i&&j<tot;j++) { st[prime[j]*i]=true; if(i%prime[j]==0) { phi[prime[j]*i]=phi[i]*prime[j]; break; } phi[prime[j]*i]=phi[i]*(prime[j]-1); } } }
五:
1:欧拉定理,也称费马-欧拉定理,是一个关于同余的性质。
如果n,a为正整数,而且互质,那么有:

当n是质数时,有:a^(n-1)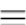 1(modn)->费马定理
1(modn)->费马定理