来自y总:
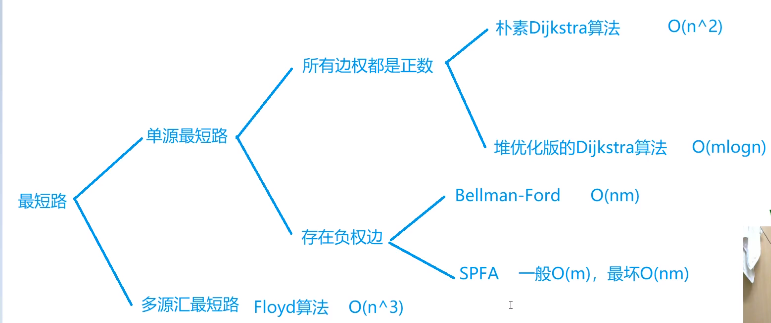
1:Floyd
三个for,枚举每一个点当做中转点对两点之间的距离进行松弛。其实就是个动态规划

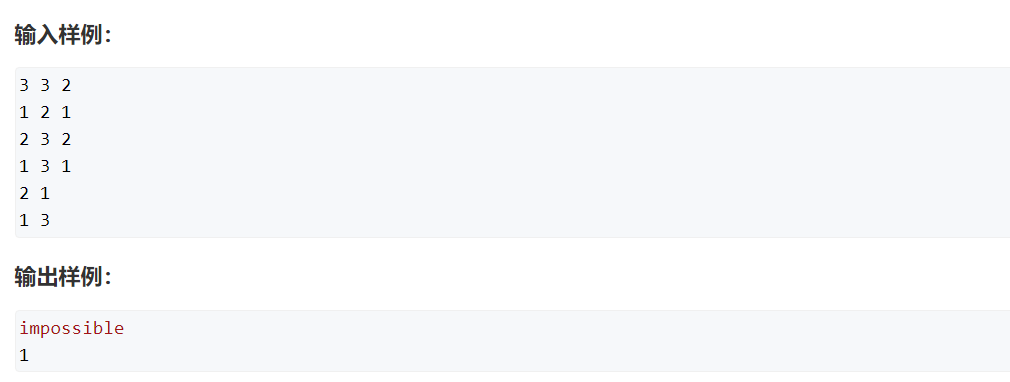
#include<iostream> #include<cstring> #include<cstdio> #include<bitset> #include<queue> using namespace std; const int maxn=3e4+10; const int maxn2=2e2+10; const int inf=99999999; int e[maxn2][maxn2]; int n,m; void floyd() { for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { if(e[i][j]>e[i][k]+e[k][j]) { e[i][j]=e[i][k]+e[k][j]; } } return ; } int main() { int k; cin>>n>>m>>k; for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(i==j) e[i][j]=0; else e[i][j]=inf; } } for(int i=1;i<=m;i++) { int a,b,c; cin>>a>>b>>c; e[a][b]=min(e[a][b],c); } floyd(); while(k--) { int a,b; cin>>a>>b; if(e[a][b]>inf/2) cout<<"impossible"<<endl; else cout<<e[a][b]<<endl; } }
二:Dijkstra
1:原Dijkstra:
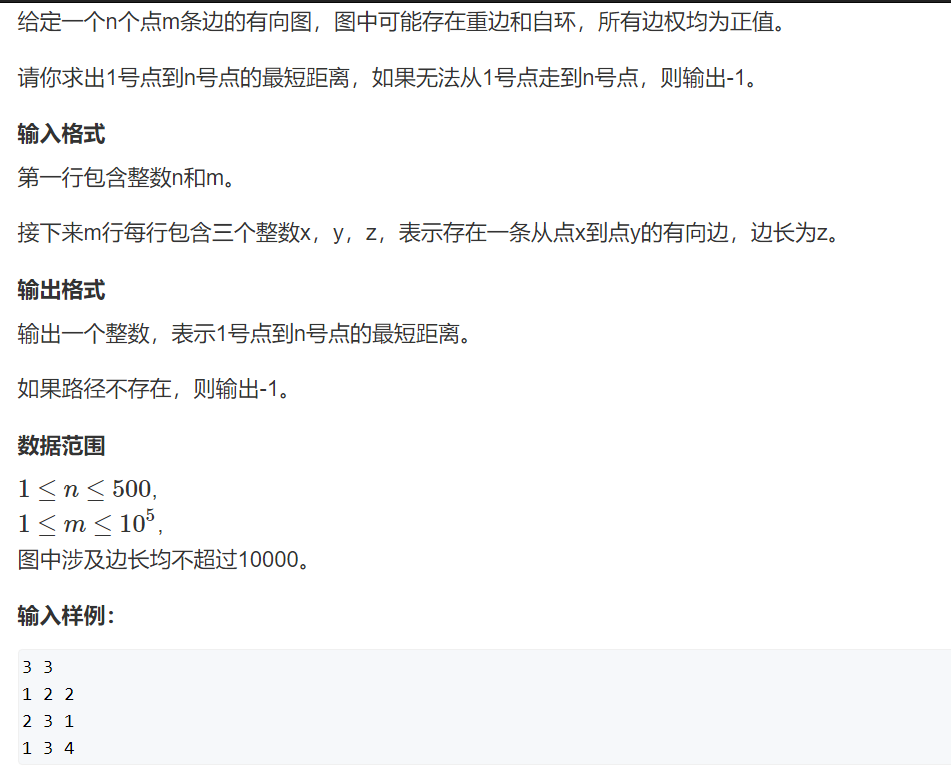
O(n*n)
#include<iostream> #include<cstring> #include<cstdio> #include<bitset> #include<algorithm> #include<queue> using namespace std; const int maxn=3e4+10; const int maxn2=5e2+10; const int inf=99999999; int e[maxn2][maxn2]; int d[maxn]; int vis[maxn]; int n,m; int main() { int k; cin>>n>>m; for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(i==j) e[i][j]=0; else e[i][j]=inf; } } for(int i=1;i<=m;i++) { int a,b,c; cin>>a>>b>>c; e[a][b]=min(e[a][b],c); } for(int i=1;i<=n;i++) { vis[i]=0; d[i]=e[1][i]; } vis[1]=1; for(int i=1;i<=n;i++) { int minn=inf,id; for(int j=1;j<=n;j++) { if(d[j]<minn&&!vis[j]) { minn=d[j]; id=j; } } vis[id]=1; for(int j=1;j<=n;j++) { d[j]=min(d[j],d[id]+e[id][j]); } } if(d[n]>inf/2) cout<<"-1"<<endl; else cout<<d[n]<<endl; // for(int i=1;i<=n;i++) // cout<<d[i]<<" "; return 0; }
2:适用于稀疏图的邻接表+堆优化版的Dijkstra
优化之前找距离1点最近的这个过程,把distance,id放入堆,每次直接O(1)就可以找出最近点。

地址:https://www.acwing.com/problem/content/852/
时间复杂度O(mlogn)
#include<iostream> #include<cstring> #include<cstdio> #include<queue> #include<algorithm> using namespace std; const int maxn=1e6; const int inf=0x3f; typedef long long ll; typedef pair<int,int>PII; int e[maxn],ne[maxn],idx,h[maxn]; int w[maxn];//权值,w[i]表示i点到其上一个点的距离 int vis[maxn];//标记 int ds[maxn];//1号点到各个点的距离 int n,m; void add(int a,int b,int c) { w[idx]=c; e[idx]=b; ne[idx]=h[a]; h[a]=idx++; } int dijk() { memset(ds,0x3f,sizeof(ds)); priority_queue<PII,vector<PII>,greater<PII>> heap;//小根堆 ds[1]=0; heap.push({0,1});//初始1号点,离自己距离为0 while(!heap.empty()) { auto t=heap.top(); heap.pop(); int distance=t.first,id=t.second; if(vis[id]==1) //避免后续不必要的操作,因为此时已经最小。避免超时 continue; vis[id]=1; for(int i=h[id];i!=-1;i=ne[i]) { int j=e[i];//获取结点对应的几号点 //cout<<ds[j]<<endl; if(ds[j]>distance+w[i]) { // cout<<id<<"-"<<e[i]<<endl; ds[j]=distance+w[i]; //1~j不如1~id~j近,则更新,注意是w[i]不是w[j],至于为什么,看add()就好了。 heap.push({ds[j],j}); } } } if(ds[n]==0x3f3f3f3f) return -1; return ds[n]; } int main() { cin>>n>>m; memset(h,-1,sizeof(h)); for(int i=1;i<=m;i++) { int a,b,c; cin>>a>>b>>c; add(a,b,c); } cout<<dijk()<<endl; return 0; }