poj 1330(初探LCA)

Nearest Common Ancestors

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 23795		Accepted: 12386

Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:


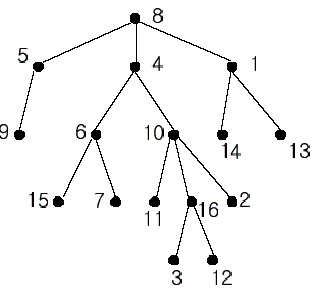
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.

Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5

Sample Output

4
3

Source

下面这段模板代码引自某位大神的博客 http://www.cppblog.com/menjitianya/archive/2015/12/10/212447.html

void LCA_Tarjan(int u) { 

        make_set(u);                               // 注释1

        ancestor[ find(u) ] = u;                   // 注释2

        for(int i = 0; i < edge[u].size(); i++) {  // 注释3

            int v = edge[u][i].v; 

            LCA_Tarjan(v);                         // 注释4

            merge(u, v);                           // 注释5

            ancestor[ find(u) ] = u;               // 注释6

        }

        colors[u] = 1;                             // 注释7

        for(int i = 0; i < lcaInfo[u].size(); i++) {

            int v = lcaInfo[u][i].v;

            if(colors[v]) {                        // 注释8

                lcaDataAns[ lcaInfo[u][i].idx ].lca = ancestor[ find(v) ];

            }

        }

    }

    注释1:创建一个集合，集合中只有一个元素u，即{ u }

    注释2:因为u所在集合只有一个元素，所以也可以写成ancestor[u] = u

    注释3:edge[u][0...size-1]存储的是u的直接子结点

    注释4:递归计算u的所有直接子结点v

    注释5:回溯的时候进行集合合并，将以v为根的子树和u所在集合进行合并

    注释6:对合并完的集合设置集合对应子树的根结点，find(u)为该集合的代表元

    注释7:u为根的子树访问完毕，设置结点颜色

    注释8:枚举所有和u相关的询问(u, v)，如果以v为根的子树已经访问过，那么ancestor[find(v)]肯定已经计算出来，并且必定是u和v的LCA

 

对于注释8的for循环,这个题只查询两个点，没必要用另外一个邻接表了

 

//题意:t组测试用例,输入n,接下来输入n-1条边 组成一棵树，第n组数据代表询问a b之间最近公共祖先
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <vector>
using namespace std;
const int MAX = 10005;
vector<int> mp[MAX];
int father[MAX];
int indegree[MAX];  ///入度为0的就是根节点
int _rank[MAX];  ///利用启发式合并防止树成链
int vis[MAX];
int ances[MAX];
int A,B;
void init(int n){
    for(int i=1;i<=n;i++){
        ances[i]=0;
        vis[i]=0;
        _rank[i] = 0;
        indegree[i]=0;
        father[i] = i;
        mp[i].clear();
    }
}
int _find(int x){
    if(x==father[x]) return x;
    return father[x] = _find(father[x]);
}
void _union(int a,int b){
    int x = _find(a);
    int y = _find(b);
    father[x]=y;
}
 int Tarjan(int u)
 {
     for (int i=0;i<mp[u].size();i++)
     {
         Tarjan(mp[u][i]);
         _union(u,mp[u][i]);
         ances[_find(u)]=u;
     }
     vis[u]=1;
    if (A==u && vis[B]) printf("%d
",ances[_find(B)]);
     else if (B==u && vis[A]) printf("%d
",ances[_find(A)]);
     return 0;
 }
int main()
{
    int tcase;
    scanf("%d",&tcase);
    while(tcase--){
        int n;
        scanf("%d",&n);
        init(n);
        int a,b;
        for(int i=1;i<n;i++){
            scanf("%d%d",&a,&b);
            mp[a].push_back(b);
            indegree[b]++;
        }
        scanf("%d%d",&A,&B);
        for(int i=1;i<=n;i++){
            if(indegree[i]==0){
               Tarjan(i);
                break;
            }
        }
    }
    return 0;
}