Max Sequence
| Time Limit: 3000MS | Memory Limit: 65536K | |
| Total Submissions: 16850 | Accepted: 7054 |
Description
Give you N integers a1, a2 ... aN (|ai| <=1000, 1 <= i <= N).
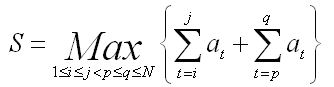
You should output S.
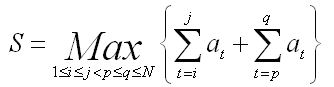
You should output S.
Input
The
input will consist of several test cases. For each test case, one
integer N (2 <= N <= 100000) is given in the first line. Second
line contains N integers. The input is terminated by a single line with N
= 0.
Output
For each test of the input, print a line containing S.
Sample Input
5 -5 9 -5 11 20 0
Sample Output
40
Source
求解序列中两段不相交的子序列的最大和。
先正着扫描 1- n-1 区间求出每个段的最大值,然后反着扫描 n - 2这段区间求出每个段的最大值,然后枚举1 - n-1 每个段,得到最大值
#include <stdio.h> #include <iostream> #include <string.h> #include <math.h> #include <algorithm> using namespace std; const int N = 100005; int a[N]; int dp[N],dp1[N]; ///dp[i]第 1-i段的最大和 , dp1[i] 第 i - n段的最大和 int main() { int n; while(scanf("%d",&n)!=EOF&&n){ for(int i=1;i<=n;i++) scanf("%d",&a[i]); int sum=0,mx = -100000000; ///每个数都有可能是负数 for(int i=1;i<n;i++){ ///因为题目中两段不能重合,所以不能枚举到n sum +=a[i]; if(sum>mx) mx = sum; if(sum<0){ sum = 0; } dp[i]=mx; } //for(int i=1;i<=n;i++) printf("%d ",dp[i]); sum = 0,mx = -100000000; for(int i=n;i>1;i--) ///因为题目中两段不能重合,所以不能枚举到1 { sum+=a[i]; if(sum>mx) mx = sum; if(sum<0) sum = 0; dp1[i] =mx; } //for(int i=1;i<=n;i++) printf("%d ",dp1[i]); mx = -100000000; for(int i=1;i<n;i++){ if(dp[i]+dp1[i+1]>mx){ mx = dp[i]+dp1[i+1]; } } printf("%d ",mx); } return 0; }