poj 2826(好坑,线段相交问题)

An Easy Problem?!

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 11576		Accepted: 1760

Description

It's raining outside. Farmer Johnson's bull Ben wants some rain to water his flowers. Ben nails two wooden boards on the wall of his barn. Shown in the pictures below, the two boards on the wall just look like two segments on the plane, as they have the same width.

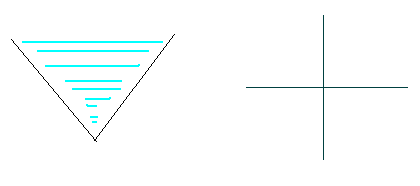
Your mission is to calculate how much rain these two boards can collect.

Input

The first line contains the number of test cases.
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x₁, y₁, x₂, y₂, x₃, y₃, x₄, y₄. (x₁, y₁), (x₂, y₂) are the endpoints of one board, and (x₃, y₃), (x₄, y₄) are the endpoints of the other one.

Output

For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected.

Sample Input

2
0 1 1 0
1 0 2 1

0 1 2 1
1 0 1 2

Sample Output

1.00
0.00

一点都不easy...

没能AC的看看吧。。

discuss里面参考数据：

9
样例一：
6259 2664 8292 9080 1244 2972 9097 9680
答案：6162.65

样例二：
0 1 1 0
1 0 2 1
答案：1.00

样例三：
0 1 2 1
1 0 1 2
答案：0.00

样例四：
0 0 10 10
0 0 9 8
答案：0.00

样例五：
0 0 10 10
0 0 8 9
答案：4.50

样例六： //这组数据其实我没过也AC了
0.9 3.1 4 0
0 3 2 2
答案：0.50

样例七：
0 0 0 2
0 0 -3 2
答案：3.00

样例八：
1 1 1 4
0 0 2 3
答案：0.75

样例九：
1 2 1 4
0 0 2 3
答案：0.00

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
const double eps = 1e-8;
struct Point
{
    double x,y;
};
double cross(Point a,Point b,Point c)
{
    return (a.x-c.x)*(b.y-c.y)-(a.y-c.y)*(b.x-c.x);
}
///规范相交
bool isCross(Point a,Point b,Point c,Point d)
{
    if(cross(c,b,a)*cross(b,d,a)<-eps) return false; ///这里要改成eps我上面的那组数据才能为0.5..不过是0也能AC。。so strange
    if(cross(a,d,c)*cross(d,b,c)<-eps) return false;
    return true;
}
///计算两条直线的交点
Point intersection(Point a,Point b,Point c,Point d)
{
    Point p = a;
    double t = ((a.x-c.x)*(c.y-d.y)-(a.y-c.y)*(c.x-d.x))/((a.x-b.x)*(c.y-d.y)-(a.y-b.y)*(c.x-d.x));
    p.x +=(b.x-a.x)*t;
    p.y +=(b.y-a.y)*t;
    return p;
}
int main()
{
    int tcase;
    scanf("%d",&tcase);
    while(tcase--)
    {
        Point a,b,c,d;
        scanf("%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y);
        scanf("%lf%lf%lf%lf",&c.x,&c.y,&d.x,&d.y);
        if(a.y==b.y||c.y==d.y||!isCross(a,b,c,d))  ///排除水平放置还有不相交的情况
        {
            printf("0.00
");
            continue;
        }
        Point p = intersection(a,b,c,d); ///交点
        double y = min(max(a.y,b.y),max(c.y,d.y));
        if(y<=p.y)  ///上面的y不可能小于交点,不然接不到水
        {
            printf("0.00
");
            continue;
        }
        ///我只要y上面的点
        Point t1,t2;
        if(a.y>b.y) t1 = a;
        else t1 = b;
        if(c.y>d.y) t2 = c;
        else t2 = d;
        ///两个向量极角大的x坐标必定小于极角小的，不然雨水没办法流进去
        if(cross(t1,t2,p)>0&&t1.x>t2.x||cross(t2,t1,p)>0&&t2.x>t1.x)
        {
            double k,B,x,x0;
            if(y==t1.y)
            {
                x = t1.x;
                if(t2.x==p.x) ///这里略坑
                {
                    x0 = p.x;
                }
                else
                {
                    k = (t2.y- p.y)/(t2.x - p.x);
                    B = t2.y-k*t2.x;
                    x0 = (y-B)/k;
                }
            }
            else
            {
                x = t2.x;
                if(t1.x==p.x)
                {
                    x0 = p.x;
                }
                else
                {
                    k = (t1.y- p.y)/(t1.x - p.x);
                    B = t1.y-k*t1.x;
                    x0 = (y-B)/k;
                }

            }
            double l = fabs(x-x0);
            double h = fabs(y-p.y);
            printf("%.2lf
",l*h/2);
            continue;
        }
        printf("0.00
");
    }
    return 0;
}