Solitaire
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4122 Accepted Submission(s): 1245
Problem Description
Solitaire
is a game played on a chessboard 8x8. The rows and columns of the
chessboard are numbered from 1 to 8, from the top to the bottom and from
left to right respectively.
There are four identical pieces on the board. In one move it is allowed to:
> move a piece to an empty neighboring field (up, down, left or right),
> jump over one neighboring piece to an empty field (up, down, left or right).
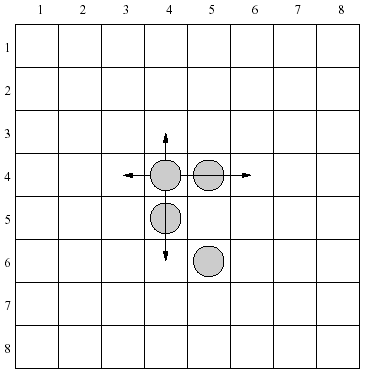
There are 4 moves allowed for each piece in the configuration shown above. As an example let's consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right.
Write a program that:
> reads two chessboard configurations from the standard input,
> verifies whether the second one is reachable from the first one in at most 8 moves,
> writes the result to the standard output.
There are four identical pieces on the board. In one move it is allowed to:
> move a piece to an empty neighboring field (up, down, left or right),
> jump over one neighboring piece to an empty field (up, down, left or right).

There are 4 moves allowed for each piece in the configuration shown above. As an example let's consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right.
Write a program that:
> reads two chessboard configurations from the standard input,
> verifies whether the second one is reachable from the first one in at most 8 moves,
> writes the result to the standard output.
Input
Each
of two input lines contains 8 integers a1, a2, ..., a8 separated by
single spaces and describes one configuration of pieces on the
chessboard. Integers a2j-1 and a2j (1 <= j <= 4) describe the
position of one piece - the row number and the column number
respectively. Process to the end of file.
Output
The
output should contain one word for each test case - YES if a
configuration described in the second input line is reachable from the
configuration described in the first input line in at most 8 moves, or
one word NO otherwise.
Sample Input
4 4 4 5 5 4 6 5
2 4 3 3 3 6 4 6
Sample Output
YES
题意:给定4个点的初始状态,点每次移动可以有两种方式。一种是如果相邻点是空的,移动到相邻点,如果相邻点非空,并且相邻点同一个方向没有点,则可以跳过去到下一个点,问8步以内能否移动到目标状态??
题解:4个点可以想到用8维数组保存状态,,但是一定要压缩压缩再压缩,强剪枝。。自己代码剪枝没通过,参考的大神的,,不过双向BFS好像快些。。而且只能用G++交才能AC。
#include<stdio.h> #include<queue> #include<iostream> #include <string.h> #include <algorithm> #include <map> using namespace std; typedef long long LL; struct Node{ int x[4],y[4]; int step; }s,t; int graph[10][10]; bool vis[8][8][8][8][8][8][8][8]; bool equals(Node a){ ///这个地方开始想错了,以为是每一个点的状态对应下一行每一行的状态,结果是只要能到达目标 ///状态就OK,比如说是起始地第二个点到达目标的第一个点 for(int i=0;i<4;i++){ if(!graph[a.x[i]][a.y[i]]) return false; } return true; } bool check(Node a){ for(int i=0;i<4;i++){ if(a.x[i]<0||a.x[i]>=8||a.y[i]<0||a.y[i]>=8) return false; } if(vis[a.x[0]][a.y[0]][a.x[1]][a.y[1]][a.x[2]][a.y[2]][a.x[3]][a.y[3]]) return false; return true; } bool cango(Node next,int k){ for(int i=0;i<4;i++){ if(i!=k&&next.x[i]==next.x[k]&&next.y[i]==next.y[k]) return false; } return true; } int dir[][2] = {{1,0},{-1,0},{0,1},{0,-1}}; bool bfs(){ queue<Node> q; q.push(s); s.step = 0; while(!q.empty()){ Node now = q.front(); q.pop(); if(now.step>8){ return false; } if(equals(now)){ return true; } for(int i=0;i<4;i++){ for(int j=0;j<4;j++){ Node next = now; next.x[i] = now.x[i]+dir[j][0]; next.y[i] = now.y[i]+dir[j][1]; next.step = now.step+1; if(next.step>8) continue; ///大神的剪枝是>=8 if(!check(next)) continue; if(cango(next,i)){ if(equals(next)) return true; vis[next.x[0]][next.y[0]][next.x[1]][next.y[1]][next.x[2]][next.y[2]][next.x[3]][next.y[3]] = true; q.push(next); } else{ next.x[i] = now.x[i]+2*dir[j][0]; next.y[i] = now.y[i]+2*dir[j][1]; if(!check(next)) continue; if(cango(next,i)){ if(equals(next)) return true; vis[next.x[0]][next.y[0]][next.x[1]][next.y[1]][next.x[2]][next.y[2]][next.x[3]][next.y[3]] = true; q.push(next); } } } } } return false; } int main() { while(scanf("%d%d",&s.x[0],&s.y[0])!=EOF){ memset(graph,0,sizeof(graph)); s.x[0]-=1,s.y[0]-=1; for(int i=1;i<4;i++){ scanf("%d%d",&s.x[i],&s.y[i]); s.x[i]--; s.y[i]--; } for(int i=0;i<4;i++){ scanf("%d%d",&t.x[i],&t.y[i]); t.x[i]--; t.y[i]--; graph[t.x[i]][t.y[i]] = 1; } memset(vis,false,sizeof(vis)); vis[s.x[0]][s.y[0]][s.x[1]][s.y[1]][s.x[2]][s.y[2]][s.x[3]][s.y[3]] = true; bool flag = bfs(); if(flag) printf("YES "); else printf("NO "); } return 0; }
双广的话非常快,主要是怎么处理初始状态和目标状态,因为有可能第1个最后跳到二状态去了,这里的解决办法是排个序之后就解决了。
#include<stdio.h> #include<queue> #include<iostream> #include <string.h> #include <algorithm> #include <map> using namespace std; typedef long long LL; struct Point{ int x,y; }; struct Node{ Point p[4]; int step; }s,t; char vis[8][8][8][8][8][8][8][8]; int graph[10][10]; int cmp(Point a,Point b){ if(a.x==b.x) return a.y<b.y; return a.x<b.x; } void make_vis(Node s,char c){ vis[s.p[0].x][s.p[0].y][s.p[1].x][s.p[1].y][s.p[2].x][s.p[2].y][s.p[3].x][s.p[3].y] = c; } char checkvis(Node s){ return vis[s.p[0].x][s.p[0].y][s.p[1].x][s.p[1].y][s.p[2].x][s.p[2].y][s.p[3].x][s.p[3].y]; } void make_graph(Node s){ memset(graph,0,sizeof(graph)); for(int i=0;i<4;i++){ graph[s.p[i].x][s.p[i].y] = 1; } } bool check(Node s){ for(int i=0;i<4;i++){ if(s.p[i].x<0||s.p[i].x>=8) return false; if(s.p[i].y<0||s.p[i].y>=8) return false; } return true; } int dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}}; bool bfs(){ memset(vis,0,sizeof(vis)); make_vis(s,'1'); make_vis(t,'2'); queue<Node> q1,q2; q1.push(s); q2.push(t); while(!q1.empty()||!q2.empty()){ if(!q1.empty()){ Node now = q1.front(); q1.pop(); if(now.step>=4) continue; make_graph(now); for(int i=0;i<4;i++){ for(int j=0;j<4;j++){ Node next = now; next.p[i].x += dir[j][0]; next.p[i].y += dir[j][1]; next.step++; if(!check(next)) continue; if(graph[next.p[i].x][next.p[i].y]){ next.p[i].x += dir[j][0]; next.p[i].y += dir[j][1]; if(!check(next)||graph[next.p[i].x][next.p[i].y]) continue; } sort(next.p,next.p+4,cmp); if(checkvis(next)=='1') continue; else if(checkvis(next)=='2') return true; make_vis(next,'1'); q1.push(next); } } } if(!q2.empty()){ Node now = q2.front(); q2.pop(); if(now.step>=4) continue; make_graph(now); for(int i=0;i<4;i++){ for(int j=0;j<4;j++){ Node next = now; next.p[i].x += dir[j][0]; next.p[i].y += dir[j][1]; next.step++; if(!check(next)) continue; if(graph[next.p[i].x][next.p[i].y]){ next.p[i].x += dir[j][0]; next.p[i].y += dir[j][1]; if(!check(next)||graph[next.p[i].x][next.p[i].y]) continue; } sort(next.p,next.p+4,cmp); if(checkvis(next)=='2') continue; else if(checkvis(next)=='1') return true; make_vis(next,'2'); q2.push(next); } } } } return false; } int main() { while(scanf("%d%d",&s.p[0].x,&s.p[0].y)!=EOF){ memset(graph,0,sizeof(graph)); s.p[0].x-=1,s.p[0].y-=1; for(int i=1;i<4;i++){ scanf("%d%d",&s.p[i].x,&s.p[i].y); s.p[i].x--; s.p[i].y--; } for(int i=0;i<4;i++){ scanf("%d%d",&t.p[i].x,&t.p[i].y); t.p[i].x--; t.p[i].y--; } s.step = t.step = 0; sort(s.p,s.p+4,cmp); sort(t.p,t.p+4,cmp); bool flag = bfs(); if(flag) printf("YES "); else printf("NO "); } return 0; }