求对于 (n) 个数的排列 , 有多少种方案满足对于所有的 (i) , (|P_i - i| != K) , 答案对 (924844033) 取模 .
(n,K le 2000)
设 (g[i]) 表示至少有 (i) 个数不满足题意的方案数 , 则 (ans = sum_{i=0}^n (-1)^{i} g[i]) .
可以画一个二分图 , 左边表示下标 , 右边表示取值 , 相隔 (K) 格的左右连一条边 . 网上有一个图 :
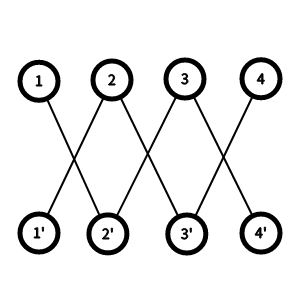
对于每一条链 , 每个点只能连一条边 . 所以在每一条链上有转移 : 设 (f[i][j][0/1]) 表示选到第 (i) 个数 , 已经连了 (j) 条边 , (i) 与 (i-1) 是否连边的方案数 , 在链的内部转移 .
对于所有的链 , 可以拼接在一起 , 链之间也可以转移 (f[i][j][0]) 的方案数 , 这就相当于继承之前的结果继续 (DP) .
要特别注意的是 , 拼接的链的长度是 (2n) .
时间复杂度 (O((2n)^2))
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cassert>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define Debug(x) cout<<#x<<"="<<x<<endl
using namespace std;
typedef long long LL;
const int INF=1e9+7;
inline LL read(){
register LL x=0,f=1;register char c=getchar();
while(c<48||c>57){if(c=='-')f=-1;c=getchar();}
while(c>=48&&c<=57)x=(x<<3)+(x<<1)+(c&15),c=getchar();
return f*x;
}
const int N = 4005;
const int mod = 924844033;
int a[N], g[N], f[N][N][2], fac[N];
int n, K, cnt, ans;
inline int add(int x, int y){return (x+y)%mod;}
inline int dec(int x, int y){return (x-y+mod)%mod;}
inline int mul(LL x, int y){return x*y%mod;}
int main(){
n = read(), K = read();
fac[0] = fac[1] = 1;
for(int i = 2; i <= n; ++i) fac[i] = mul(fac[i-1], i);
for(int i = 1; i <= K; ++i){
for(int j = i; j <= n; j += K)
a[++cnt] = j;
for(int j = i; j <= n; j += K)
a[++cnt] = j;
}
assert(cnt == (n << 1));
f[1][0][0] = 1;
for(int i = 2; i <= (n << 1); ++i){
for(int j = 0; j <= min(n, i/2); ++j){
f[i][j][0] = add(f[i-1][j][0], f[i-1][j][1]);
if(j > 0 && a[i] - a[i-1] == K) f[i][j][1] = f[i-1][j-1][0];
}
}
for(int i = 0; i <= n; ++i){
g[i] = add(f[n << 1][i][0], f[n << 1][i][1]);
if(!(i&1)) ans = add(ans, mul(g[i], fac[n - i]));
else ans = dec(ans, mul(g[i], fac[n - i]));
}
printf("%d
", ans);
}
(CF) 上还有一篇讨论 , 是这题的 (NTT) 做法 : Solve AGC005D with NTT