快速排序(Quicksort)是对冒泡排序的一种改进。
它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。快速排序的核心思想是二分查找,找出一个中间值,使得比该中间值大的值均在其右侧,比该中间值小的值均在其左侧,并且递归执行,从而达到有序排列。二分查找相当于构造一颗红黑树,从而实现元素的有序排列:
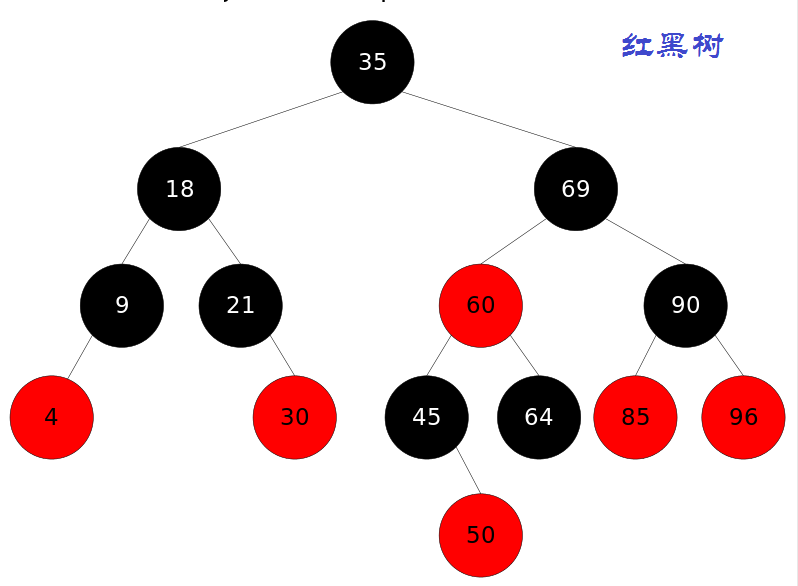
【注1:红黑树的实质,是在一组待排序的数据中,找出一个处于中间位置的值,比该值小的数据位于其左下侧,比该值大的数据位于其右下侧;以此类推。由于选用了红色和黑色这两种反差明显的颜色构建了一颗数Tree,而且具备一些特点,故称为红黑树】
【注2:红黑树是一种近似平衡的二叉查找树,它能够确保任何一个节点的左右子树的高度差不会超过二者中较低那个的一陪。具体来说,红黑树是满足如下条件的二叉查找树(binary search tree):
每个节点要么是红色,要么是黑色;
根节点必须是黑色;
红色节点不能连续(也即是,红色节点的孩子和父亲都不能是红色);
对于每个节点,从该点至null(树末端)的任何路径,都含有相同个数的黑色节点。
在树的结构发生改变时(插入或者删除操作),往往会破坏上述条件3或条件4,需要通过调整使得查找树重新满足红黑树的条件。】
【注3:数的高度,是从下往上看,从1开始,最底层是1层;数的深度,是从上往下看,从0开始,只有一个根节点(为于0层),根节点下面的层数就是数的深度。一般来说,数的高度=树的深度+1。】
我们还使用上述的待排序数据集,演示快速排序。
package 排序算法.快速排序;
/**
* 快速排序
* @author 李章勇
*/
import java.util.Arrays;
public class Demo1 {
static int k = 0;
public static void quickSort(int[] arr, int _left, int _right) {
if (_left > _right) {
return;
}
int left = _left;
int right = _right;
int temp = arr[left];
while (left != right) {
while (right > left && arr[right] >= temp) {
right--;
}
arr[left] = arr[right];
while (left < right && arr[left] <= temp) {
left++;
}
arr[right] = arr[left];
}
//到此,left和right重叠相等,得到一个中间值,再继续对该中间值左右两侧的数据们进行快速排序
arr[left] = temp;
System.out.println("第" + (++k) + " 次:" + Arrays.toString(arr));
quickSort(arr, _left, left - 1);
quickSort(arr, left + 1, _right);
}
public static void main(String[] args) {
int[] arr = new int[]{15, 32, 14, 86, 54, 78, 36};
System.out.println("排序前的数组:" + Arrays.toString(arr));
quickSort(arr, 0, arr.length - 1);
System.out.println("排序后的数组:" + Arrays.toString(arr));
}
}
上述代码运行后,结果如下:
排序前的数组:[15, 32, 14, 86, 54, 78, 36] 第1 次:[14, 15, 32, 86, 54, 78, 36] 第2 次:[14, 15, 32, 86, 54, 78, 36] 第3 次:[14, 15, 32, 86, 54, 78, 36] 第4 次:[14, 15, 32, 36, 54, 78, 86] 第5 次:[14, 15, 32, 36, 54, 78, 86] 第6 次:[14, 15, 32, 36, 54, 78, 86] 第7 次:[14, 15, 32, 36, 54, 78, 86] 排序后的数组:[14, 15, 32, 36, 54, 78, 86]
接下来,我再对上述代码进行优化:
package 排序算法.快速排序;
import java.util.Arrays;
/**
* 快速排序的优化;本质上是二分查找
*/
public class Test {
static int k=0;
static void quickSort(int[] arr,int _left,int _right){
//左右两个指针,要确保左指针不能大于右指针,否则不和逻辑;如果左右指针相等,说明数组里只有一个元素,无需排序
if(_left>=_right){
return;
}
// System.out.println(_left+"--"+_right);
boolean boo=true;//默认全部有序,为true
for(int i=_left;i<_right;i++){
//如果arr[_left]不是最小值,则意味着出现无序
if(arr[_left]>arr[i+1]){
boo=false;
}
}
if(boo){
quickSort(arr,_left+1,_right);
return;
}
int left=_left;
int right=_right;
int temp=arr[left];
while(left!=right){//即左指针小于右指针时
while(right>left && arr[right]>=temp){//从右指针开始向左移动,并且比左指针处的元素大时
right--;//右指针向左移动
}
//一旦出现右指针指向的元素小于左指针处的元素,则将小数赋予左指针处的元素
arr[left]=arr[right];
//再将左指针向右移动
while(left<right && arr[left]<=temp){
left++;
}
arr[right]=arr[left];
}
arr[left]=temp;
System.out.println("第"+(++k)+"次排序:"+ Arrays.toString(arr));
quickSort(arr,_left,left-1);
quickSort(arr,left+1,_right);
}
public static void main(String[] args) {
int[] arr=new int[]{15,32,14,86,54,78,36};
System.out.println("排序前的数组:"+Arrays.toString(arr));
quickSort(arr, 0, arr.length-1);
System.out.println("排序后的数组:"+Arrays.toString(arr));
}
}
上述代码执行结果如下:
排序前的数组:[15, 32, 14, 86, 54, 78, 36] 第1次排序:[14, 15, 32, 86, 54, 78, 36] 第2次排序:[14, 15, 32, 36, 54, 78, 86] 排序后的数组:[14, 15, 32, 36, 54, 78, 86]
最后,在时间复杂度方面,快速排序的最糟糕状况是O(n²) ,平均时间复杂度为O(n*logn)。