希尔排序

1.  希尔排序

   • 在希尔排序出现之前，计算机界普遍存在“排序算法不可能突破O(n2)”的观点。希尔排序是第一个突破O(n2)的排序算法，它是简单插入排序的改进版。

   • 希尔排序的提出，主要基于以下两点：

     • 插入排序算法在数组基本有序的情况下，可以近似达到O(n)复杂度，效率极高。

     • 但插入排序每次只能将数据移动一位，在数组较大且基本无序的情况下性能会迅速恶化。

2. 算法描述

   • 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；

   • 按增量序列个数k，对序列进行k趟排序；

   • 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序;

   • 仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

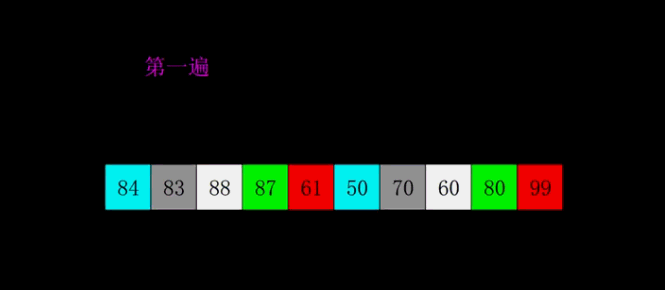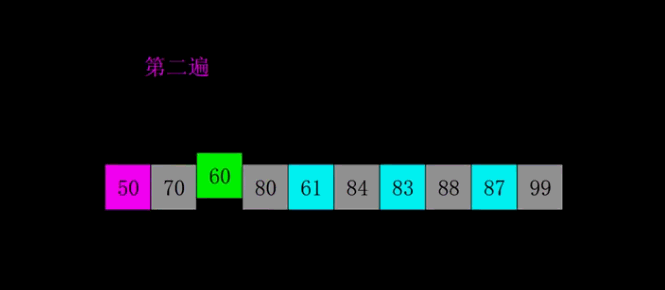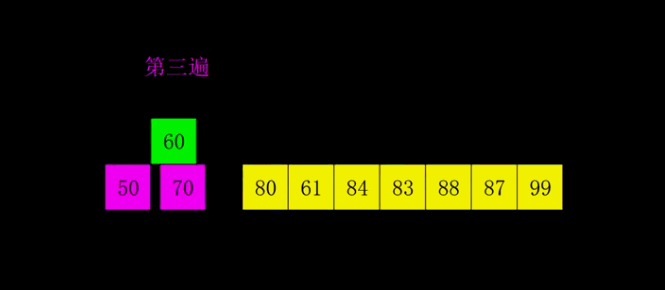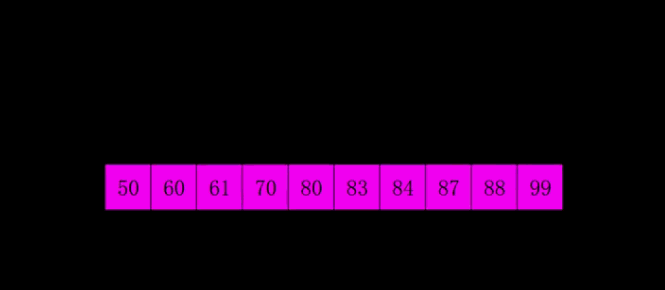
3. 动图演示

   • 

4. 算法实现
   • Donald Shell增量

     public static void shellSort(int[] arr){
         int temp;
         for (int delta = arr.length/2; delta>=1; delta/=2){//对每个增量进行一次排序
             for (int i=delta; i<arr.length; i++){              
                 for (int j=i; j>=delta && arr[j]<arr[j-delta]; j-=delta){ //注意每个地方增量和差值都是delta
                     temp = arr[j-delta];
                     arr[j-delta] = arr[j];
                     arr[j] = temp;
                 }
             }
         }
     }

   • O(n3/2) by Knuth

     public static void shellSort2(int[] arr){
         int delta = 1;
         while (delta < arr.length/3){//generate delta
             delta=delta*3+1;    // <O(n^(3/2)) by Knuth,1973>: 1, 4, 13, 40, 121, ...
         }         
         int temp;
         for (; delta>=1; delta/=3){
             for (int i=delta; i<arr.length; i++){              
                 for (int j=i; j>=delta && arr[j]<arr[j-delta]; j-=delta){
                     temp = arr[j-delta];
                     arr[j-delta] = arr[j];
                     arr[j] = temp;
                 }
             }
         }
     }

5. 希尔排序的增量

   • 希尔排序的增量数列可以任取，需要的唯一条件是最后一个一定为1（因为要保证按1有序）。但是，不同的数列选取会对算法的性能造成极大的影响。上面的代码演示了两种增量。
     切记：增量序列中每两个元素最好不要出现1以外的公因子！（很显然，按4有序的数列再去按2排序意义并不大）。
     下面是一些常见的增量序列。
     - 第一种增量是最初Donald Shell提出的增量，即折半降低直到1。据研究，使用希尔增量，其时间复杂度还是O(n2)。

     第二种增量Hibbard：{1, 3, ..., 2k-1}。该增量序列的时间复杂度大约是O(n1.5)。

     第三种增量Sedgewick增量：(1, 5, 19, 41, 109,...)，其生成序列或者是94i - 92i + 1或者是4i - 3*2i + 1。

6. 算法分析
   • 时间复杂度

     • 最佳情况：T(n) = O(n)

     • 最坏情况：T(n) = O(n2)

     • 平均情况：T(n) =O(n1.3)

   • 空间复杂度：O(1)
7. 适用场景
   •  希尔排序虽然快，但是毕竟是插入排序，其数量级并没有后起之秀--快速排序O(n㏒n)快。在大量数据面前， 希尔排序不是一个好的算法。但是，中小型规模的数据完全可以使用它。