题目:求最大连续子数组和(最大子段和)
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
-- 引用自《百度百科.》
解题程序
对问题分析过后结合代码我画出了主要流程图如下:
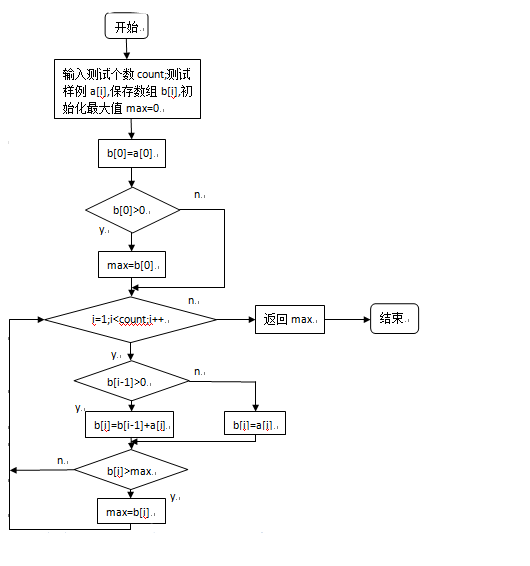
覆盖介绍:
1.语句覆盖:语句覆盖是最起码的结构覆盖要求,语句覆盖要求设计的测试用例,使得程序中每条语句至少被执行一次。
2.判定覆盖:判定覆盖又称为分支覆盖,它要求程序中每个判定至少有一次为真值,有一次为假值。
3.条件覆盖:要求设计足够多的测试用例,使得判定中的每个条件获得各种可能的结果,即每个条件至少有一次为真值,有一次为假值。
4.条件/判定覆盖:要求使得判定中每个条件的所有可能结果至少出现一次,每个判定本身所有可能结果也至少出现一次。
5.组合覆盖:要求设计足够多的测试用例,使得每个判定中条件结果的所有可能组合至少出现一次。
最终我选择了组合覆盖:(测试如下)
TEST_METHOD(TestMethod1)
{
// TODO: 在此输入测试代码
int count = 8;
int max;
int a[8] = { 10,-1,-100,5,4,3,2,1 };
max = maxsum(count, a);
Assert::AreEqual(15, max);
}
TEST_METHOD(TestMethod2)
{
// TODO: 在此输入测试代码
int count = 6;
int max;
int a[6] = {0,-1,-2,-3,-4,-5};
max = maxsum(count, a);
Assert::AreEqual(0, max);
}
TEST_METHOD(TestMethod3)
{
// TODO: 在此输入测试代码
int count = 6;
int max;
int a[6] = {1,1,2,3,-2,-1};
max = maxsum(count, a);
Assert::AreEqual(7, max);
}
TEST_METHOD(TestMethod4)
{
// TODO: 在此输入测试代码
int count = 6;
int max;
int a[6] = {1,2,3,-3,2,1};
max = maxsum(count, a);
Assert::AreEqual(6, max);
}
TEST_METHOD(TestMethod5)
{
// TODO: 在此输入测试代码
int count = 6;
int max;
int a[6] = {4,1,-2,2,-1,3};
max = maxsum(count, a);
Assert::AreEqual(7, max);
}
测试结果:
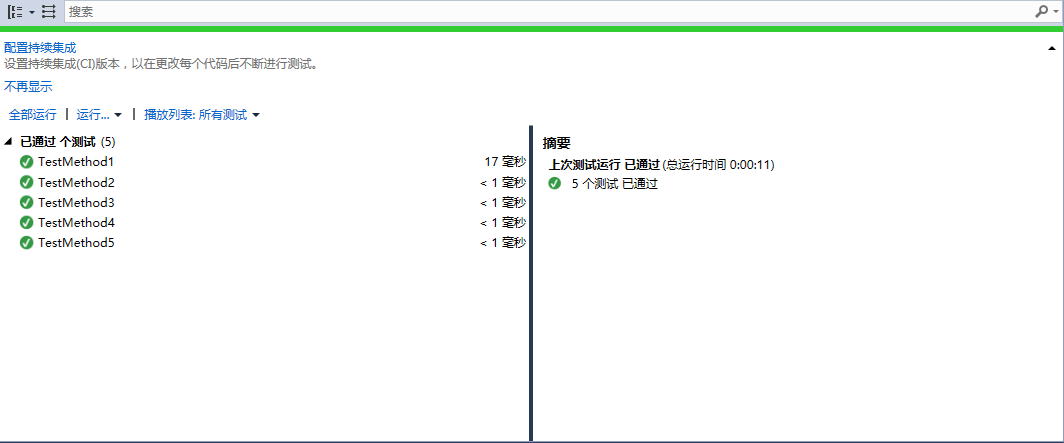
结语:
其实之前做单元测试的时候虽然做了出来,但是具体软件内部是怎么测试的还是不太清楚。对于单元测试的测试数据其实是比较难找的,只不过我们这个问题还不算复杂,虽然花了一些时间来找数据,但还算是找到了。自己对测试代码的编写也不是太懂,然后去找视频看,问同学,终于清楚了单元测试的具体流程,是怎么运行测试的,虽然花了不少时间,但是还是有收获的,接下来继续努力!对了,这里我分享一个视频,我觉得对不太清楚VS单元测试的会有一定帮助吧。