二阶行列式:2行,2列,4个元素, aij:表示第几行,第几列. 主对角线: \, 次对角线: /.
排列:由1,2,...,n组成的一个有序数组,叫做n级排列(中间不能缺数)
- n级排列: n(n-1)(n-2)......3X2X1=n!
- 逆序: 大的数排在了小数的前面构成了逆序
- 逆序数: 逆序的总数, eg: 4213: 3+1=4(4后边的逆序数:2,1,3. 2后边的逆序数:1,总共4个数)记作: N(4213) = 3+!=4
- 类似的,像: N(1,2,3,...,n)=0的这样的排列叫做标准排列(自然排列)
- N(n,n-1,...,3,2,1) = n-1 + n-2+...+ 2+1 = n(n-1)/2
- 对换:交换两个数
- 定理1: 一个兑换,排列奇偶性改变,当做奇数对换, 排列奇偶性改变, 偶数次对换, 排列奇偶性不变
- 定理: N级排列中, 奇排列,偶排列各占n!/2
n阶行列式
- 定义:
- (按行)行标取排列, 列标取排列的所有可能, 共有n!项,从不同行不同列取n个元素相乘, 符号由列标排列的奇偶性决定的.
- (按列)列取标准列, 行标取排列的所有可能, 共有n!项, 从不同的列不同行取n个元素相乘, 符号由行标排列的奇偶性决定的
- (即不按行也不按列), Σ(-1)N(i1i2...in) + (j1j2...jn)ai1j1ai2j2...ainjn
- n阶行列式的表达式: Σ(-1)N(j1,j2,...,jn)j1,j2...jna1j1a2j2...anjn
- 下三角行列式(左下角) = 主对角线相乘
- 上三角行列式(右上角) = 主对角线相乘
- 对角形行列式 = 主对角线相乘
- 下三角行列式(右下角) = (-1) N(n(n-1),...3,2,1)a1n a2(n-1),...,an1
- 上三角行列式(左上角) = (-1)N([n(n-1)]/2)a1n a2(n-1),...,an1
转置:
- 将原来的行列转换位置叫做转置, 记作:DT
- 性质1: DT = D对行成立的性质, 对列也成立
- 性质2: 两行(列)互换, 值变号
- 推论: 两行(列)相等, 行列式的值等于0即:D=0
- 性质4: 某一行都乘以K, 等于K乘以行列式的值D
- 推论: 某一行都有公因子K, k提外面, 行列式所有元素均有公因子K, k外提n次
- 性质5: 两行对应成比例, D = 0
- 推论: 某一行全为0, 则行列式的值为0,即D=0
- 性质6: 如果行列式的某一行使2个数相加,其余不变,则这个行列式=把相加的行拆开, 原行不变的2个行列式相加
- 性质7: 某一行乘以一个数, 加到另一行上去, 行列式的值不变
- 化简称上三角的的步骤:
- 先处理第一列, 再处理第二列, 再处理第三列
- 第一列处理完, 第一列不再参与运算
按行展开
- 余子式: 去掉某个元素所在的行和去掉这个元素所在的列, 剩下的行列式叫做余子式(去掉元素所在的行和列剩余的行列式, 其中剩余的行列式也是原来行列式的子集)记作: Mij(i:表示第i行, j表示第j列)
- 代数余子式: 再余子式的前边乘以-1, 记作Aij=(-1)i+j |行列式|
- 定理(按某行(列展开)):对于给定的一个行列式= 任意一个元素与其对应的代数余子式的乘积之和
- D = ai1Ai1 + ai2Ai2 + ...+ ainAin (按行展开)
- D = a1jA1j + a2jA2j + ... + anjAnj (按列展开)
- 选择0多的行(列)展开方便计算
- 定理(异乘变零):某行元素雨另一行元素的代数余子式乘积之和=0
- 拉普拉斯定理:k阶子式, 取n行n列,交叉位置上的元素构成k阶子式
- 余子式: 去掉k阶行, k阶列,剩下的行列式就叫做k阶子式的余子式
- 代数余子式: 去掉k行k列,剩下的行列式乘以(-1)k行+k列
- 取定k行,由k行元素组成的所有k阶子式与代数余子式乘积之和=D
- 行列式相乘: 同阶行列式
行列式的计算
- 三叉型行列式: 行列式中只有第一行, 第一列, 和主对角线有值,其余全是0的行列式(注意: 不能改变原行列式的值)
- 加边法: 不能改变原行列式的值
- 三叉型行列式: 一般都是用对角线取消除第一列
- 有字母:放分母,注意不等于0的条件
- 范德蒙德行列式,形如
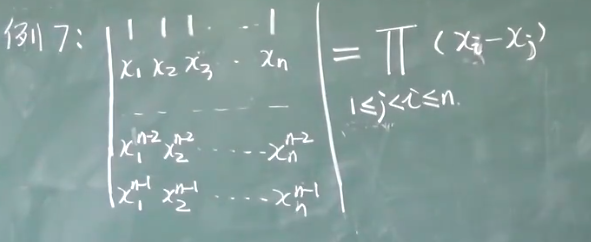
- 反对称行列式: aij = aji, aii = -aii
- 对角线全为0
- 上下位置对应成相反数
- 技术界, D =0
- 对称行列式: aij = aji, aii = aii
- 主对角线元素无要求
- 上下对应相等
克莱姆法则:(适用于:方程的个数=未知个数)
- 取方程的系数构成的行列式叫做:系数行列式
- 含有n个方程, n个未知数
- D ≠ 0 (此时的D就是系数行列式)
- Xj = Dj/D, 其中, D = 系数行列式, Dj为将方程右边的常数替换系数行列式的相应的j列
- 当方程右边的全为0的时候, 此时为齐次方程组, 齐次方程组至少有0解.
- 定理: 齐次, 方程个数=未知数的个数, D≠0, 只有零解
- 定理: 齐次方程(方程的个数=未知数个数)有非零解↔D=0