HGOI20190812 省常中互测5

　　Task 1 辩论 

有N 个参加辩论的候选人，每个人对这两个议题都有明确的态度，支持或反对。
作为组织者，小D 认真研究了每个候选人，并给每个人评估了一个非负的活跃度，
他想让活跃度之和尽可能大。
选出的候选人必须满足以下两个条件：
1. 至少有一半的人支持议题1。
2. 至少有一半的人支持议题2。
小D 想知道，在满足以上两个条件的情况下，活跃度之和最大是多少。

对于$ 100\%$ 的数据，$ N leq  4 imes  10^5，0 ≤ Ai ≤ 5 imes  10^3 $

Sol : 首先$11$的全部都可以选，然后将$01$ 和 $10$排序，依次选取，把一组最大的$10$和$10$当做$11$处理，

       剩余的情况就是$10$或$01$ $00$，这样子显然会让一个数逐渐的趋向于小于Sum/2，所以这个时候直接就挑权值大的数找即可。

　　复杂度是$O(n log_2 n)$

# include<bits/stdc++.h>
# define int long long
using namespace std;
vector<int>a1,a2,a3,a4,tmp;
int n;
signed main()
{
    scanf("%lld",&n);
    for (int i=1;i<=n;i++) {
        int op,v; scanf("%lld%lld",&op,&v);
        if (op==11) a1.push_back(v);
        else if (op==10) a2.push_back(v);
        else if (op==01) a3.push_back(v);
        else if (op==00) a4.push_back(v);
    }
    sort(a1.begin(),a1.end()); reverse(a1.begin(),a1.end());
    sort(a2.begin(),a2.end()); reverse(a2.begin(),a2.end());
    sort(a3.begin(),a3.end()); reverse(a3.begin(),a3.end());
    int num=0,ans=0,all=0;
    for (int i=0;i<a1.size();i++) num++,ans+=a1[i],all++;
    int pos;
    for (pos=0;pos<min(a2.size(),a3.size());pos++) {
        ans+=a2[pos]+a3[pos]; num++; all+=2; 
    }
    for (int i=pos;i<a2.size();i++) tmp.push_back(a2[i]);
    for (int i=pos;i<a3.size();i++) tmp.push_back(a3[i]);
    for (int i=0;i<a4.size();i++) tmp.push_back(a4[i]);
    sort(tmp.begin(),tmp.end());  reverse(tmp.begin(),tmp.end());
    for (int i=0;i<tmp.size();i++) {
        if (2*num>=all+1)  ans+=tmp[i],all++;
        else break;
    }
    printf("%lld
",ans); 
    return 0;
 }

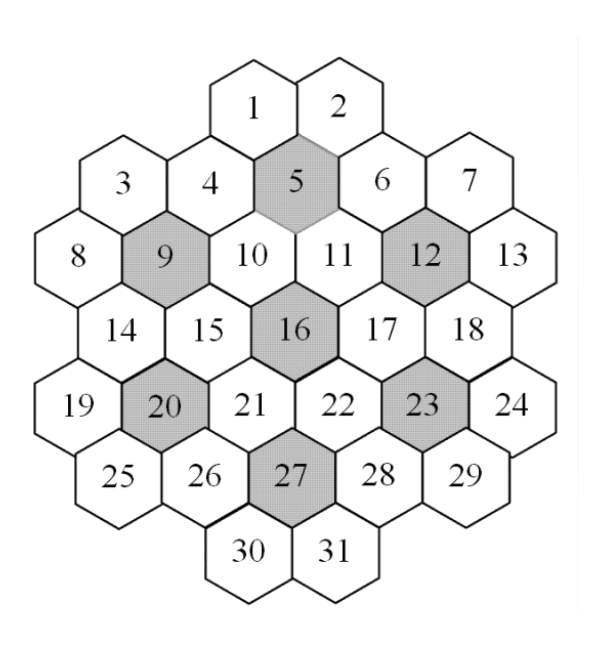
　　Task 2 数独

　　考虑一个六边形数独，3个方向的每一行都需要填不同的数，并且一个子六边形内部都需要填不同的数。

　　填写数的值域是$[1,K]$ 

　　

现在，有一些格子已经填好了数，询问字典序第$n$小的方案，

对于$ 100\%$ 的数据，$k ≤ 31,N ≤ 100000$

Sol : 直接dfs，然后对有关系的点直接存点的编号，由于数的大小为$31$所以可以用二进制数表示填是否填数，

　　这样就不用开数组模拟了，位运算非常快，然后就基本上没有优化的空间了，本题是一个NP问题。

# pragma GCC optimize(3)
# include<bits/stdc++.h>
using namespace std;
int zu[28][7]={
{1,2},{3,4,5,6,7},{8,9,10,11,12,13},{14,15,16,17,18},{19,20,21,22,23,24},{25,26,27,28,29},{30,31},
{7,13},{2,6,12,18,24},{1,5,11,17,23,29},{4,10,16,22,28},{3,9,15,21,27,31},{8,14,20,26,30},{19,25},
{3,8},{1,4,9,14,19},{2,5,10,15,20,25},{6,11,16,21,26},{7,12,17,22,27,30},{13,18,23,28,31},{24,29},
{1,2,4,5,6,10,11},{3,4,8,9,10,14,15},{6,7,11,12,13,17,18},{10,11,15,16,17,21,22},
{14,15,19,20,21,25,26},{17,18,22,23,24,28,29},{21,22,26,27,28,30,31}
};
int a[40],n,k;
vector<int>v[40]; 
int get(int pos)
{
    int lim=0;
    for (int i=1;i<v[pos].size();i++) {
        int to=a[v[pos][i]];
        lim|=(1<<to); 
    }
    return lim;
}
void dfs(int pos)
{
    if (pos==32) {
        n--;
        if (!n){
            puts("Found");
            for (int i=1;i<=31;i++) printf("%d ",a[i]);
            puts("");
            exit(0); 
        }
        return;
    }
    if (a[pos]) { dfs(pos+1); return;}
    int tmp=get(pos);
    for (int i=1;i<=k;i++) 
            if (!((1<<i)&tmp)) a[pos]=i,dfs(pos+1),a[pos]=0;
} 
int main()
{
    for (int i=0;i<28;i++) {
      for (int j=0;j<7;j++)
       if (zu[i][j]>0 && zu[i][k]>0) {
        for (int k=0;k<7;k++) if (zu[i][j]!=zu[i][k])
         v[zu[i][j]].push_back(zu[i][k]);
         v[zu[i][k]].push_back(zu[i][j]);
       }
    }
    for (int i=1;i<=31;i++) {
        sort(v[i].begin(),v[i].end());
        v[i].erase(unique(v[i].begin(),v[i].end()),v[i].end());
    }
    scanf("%d%d",&k,&n);
    for (int i=1;i<=31;i++) scanf("%d",&a[i]);
    dfs(1);
    puts("No way");
    return 0;
}