O(n2)排序
排序算法也就是我们通常说的将一组数据依照特定排序方式的一种算法。
排序算法的输出必须要遵循两个原则:
1.输出的结果为递增数列(递增针对所需的排序顺序而言)
2.输出的结果为原输入的一种排列或重组。
1.冒泡排序
顾名思义就是谁冒泡泡冒的快,上升的就快。 看下图:



相信大家一看 就很明白,首选将两个数据进行比较,遇见比自己的大的数据,接着向后找,直到找到比自己小的数据,然后进行交换,第二个数据依次论推
for i:=1 to n-1 do
for j=i+1 to n do
if a[i]>a[j]then begin
t:=a[i];
a[i]:=a[j];
a[j]:=t;
end;
2.插入排序
工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。时间复杂度同冒泡排序
主要有两个动作:操作和交换,如果操作的代价大于交换的代价,建议采用二分查找来减少比较操作的代价,二分查找是插入排序的一个变异算法。
/*插入排序 默认第一个元素是已被排序
* 取出下一个元素 在已排序的元素中进行比较
* 如果已排序的元素大于该元素 则将该元素移动到下一位置
* 直到找到小于或等于的该元素的位置
* 将该元素插入到该位置
* 如果比较操作的代价大于交换操作的话 就要考虑用二分查找法
* 最差复杂度O(N^2) 最优时间复杂度O(N) 平均时间复杂度O(N^2) 空间复杂度O(N)
* 和冒泡排序是一个级别
*/
for i:=1 to n-1 do
begin
min:=maxlongint;
for j:=i+1 to n do
if min>a[j]then
begin
min:=a[j];
min_j:=j;
end;
a[min_j]:=a[i];
a[i]:=min;
end;
综合排序:
实际上还有更好的方法,一下是我写的排序,比他们的快一些,因为交换次数少。
以数组a存储待排序元素,n为元素总个数,i,j,k,tmp为变量。
for i:=1 to n-1 do
begin
k:=i
for j:=i+1 to n do if a[k]>a[j] then k:=j;
tmp:=a[i];
a[i]:=a[k];
a[k]:=tmp;
end;
这个可以理解为冒泡,也可以理解为选择,总而言之相比于冒泡和选择快就是了。
O(n log n)排序
1、快速排序
1.归并排序
也就是合并排序,将两个或两个以上的有序数据序列合并成一个新的有序数据序列,它的基本思想是假设数组A有N个元素,那么可以看成数组A有N个有序的子序列组成,每个子序列的长度为1,然后在将两两合并,得到一个N/2个长度为2或1的有序子序列,再两两合并,如此重复,直到得到一个长度为N的有序序列为止。
例如:数组A有7个数据,分别是 23,5,69,85,26,32,15 采用归并排序算法的操作过程如下:
初始值【23】【5】【69】【85】【26】【32】【15】
第一次 会被分成两组【23】【5】 【69】,【85】【26】【32】【15】
第二次 将第一组分成【23】,【5】 【69】两组
第三次 将第二次分的第二组进行拆分【5】,【69】两组
第四次 对第三次拆分数组进行合并排序【5 69】
第五次 第四次排序好的数组和第二次拆分的数组合并为【5 23 69】
接下来 对第一次拆分的第二数组做同样的过程操作,合并为【15 26 32 85】
最后将两个有序的数组做最后的合并【5 15 23 26 32 69 85】
该算法的核心思想是采用了分治思想,即将一个数组分成若干个小数组排序,排序后再两两合并的过程。
首先看合并的过程实现,上代码:ans是逆序对别管他!
procedure MergeSort(l,r:longint); var i,j,k,mid:longint; t:array[0..40000]of longint; begin if l=r then exit; mid:=(l+r)div 2; MergeSort(l,mid); MergeSort(mid+1,r); i:=l;j:=mid+1;k:=l; while(i<=mid) and (j<=r)do if(a[i]>a[j])then begin t[k]:=a[j];inc(k);inc(j);inc(ans,mid-i+1);end else begin t[k]:=a[i];inc(k);inc(i);end; while (i<=mid) do begin t[k]:=a[i];inc(k);inc(i);end; while (j<=r) do begin t[k]:=a[j];inc(k);inc(j);end; for i:=l to r do a[i]:=t[i]; End;
这个是基于关键字比较在最坏情况下的最好时间复杂度,计算过程:
因为一次比较可以区分数据的两个状态,n个数据的初始排列可能为n!,用完全二叉树来看,n!个叶子的高度为O(log2(n!))~O(nlog2n)
2.快速排序
在平均状况下,排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较,但这种状况并不常见。事实上,快速排序通常明显比其他Ο(n log n) 算法更快,因为它的内部循环可以在大部分的架构上很有效率地被实现出来,且在大部分真实世界的数据,可以决定设计的选择,减少所需时间的二次方项之可能性。
快速排序使用分治法策略来把一个串行分为两个子串行。
步骤为:
- 从数列中挑出一个元素,称为 "基准",
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区操作。
- 递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代中,它至少会把一个元素摆到它最后的位置去。
看图:

上代码:
procedure qsort(l,r:longint); var i,j,mid:longint; begin i:=l; j:=r; mid:=a[(l+r)>>1]; repeat while a[i]<mid do inc(i); while a[j]>mid do dec(j); if i<=j then begin swap(a[i],a[j]); inc(i); dec(j); end; until i>=j; if l<j then qsort(l,j); if i<r then qsort(i,r); end;
在最优情况下,Partition每次都划分得很均匀,如果排序n个关键字,其递归树的深度就为 [log2n]+1( [x] 表示不大于 x 的最大整数),即仅需递归 log2n 次,需要时间为T(n)的话,第一次Partiation应该是需要对整个数组扫描一遍,做n次比较。然后,获得的枢轴将数组一分为二,那么各自还需要T(n/2)的时间(注意是最好情况,所以平分两半)。于是不断地划分下去,就有了下面的不等式推断:
这说明,在最优的情况下,快速排序算法的时间复杂度为O(nlogn)。
2、最糟糕情况
然后再来看最糟糕情况下的快排,当待排序的序列为正序或逆序排列时,且每次划分只得到一个比上一次划分少一个记录的子序列,注意另一个为空。如果递归树画出来,它就是一棵斜树。此时需要执行n‐1次递归调用,且第i次划分需要经过n‐i次关键字的比较才能找到第i个记录,也就是枢轴的位置,因此比较次数为 ,最终其时间复杂度为O(n^2)。
3、一般情况
最后来看一下一般情况,平均的情况,设枢轴的关键字应该在第k的位置(1≤k≤n),那么:
本来想按这种思路推导出来,结果发现半天推不出结果,最后去翻阅《算法导论》7.4节,发现证明过程还是蛮复杂的,我就偷懒贴一下好了~
O(n)排序
桶排序
1,桶排序是稳定的
2,桶排序是常见排序里最快的一种,比快排还要快…大多数情况下
3,桶排序非常快,但是同时也非常耗空间,基本上是最耗空间的一种排序算法
我自己的理解哈,可能与网上说的有一些出入,大体都是同样的原理
无序数组有个要求,就是成员隶属于固定(有限的)的区间,如范围为[0-9](考试分数为1-100等)
例如待排数字[6 2 4 1 5 9]
准备10个空桶,最大数个空桶
[6 2 4 1 5 9] 待排数组
[0 0 0 0 0 0 0 0 0 0] 空桶
[0 1 2 3 4 5 6 7 8 9] 桶编号(实际不存在)
1,顺序从待排数组中取出数字,首先6被取出,然后把6入6号桶,这个过程类似这样:空桶[ 待排数组[ 0 ] ] = 待排数组[ 0 ]
[6 2 4 1 5 9] 待排数组
[0 0 0 0 0 0 6 0 0 0] 空桶
[0 1 2 3 4 5 6 7 8 9] 桶编号(实际不存在)
2,顺序从待排数组中取出下一个数字,此时2被取出,将其放入2号桶,是几就放几号桶
[6 2 4 1 5 9] 待排数组
[0 0 2 0 0 0 6 0 0 0] 空桶
[0 1 2 3 4 5 6 7 8 9] 桶编号(实际不存在)
3,4,5,6省略,过程一样,全部入桶后变成下边这样
[6 2 4 1 5 9] 待排数组
[0 1 2 0 4 5 6 0 0 9] 空桶
[0 1 2 3 4 5 6 7 8 9] 桶编号(实际不存在)
0表示空桶,跳过,顺序取出即可:1 2 4 5 6 9
以下代码仅供参考(开了去重排序)
var f:array[0..100000] of boolean; n,i,x,s:longint; BEGIN fillchar(f,sizeof(f),false); readln(n); for i:=1 to n do begin read(x);f[x]:=true; end;s:=0; for i:=0 to 100000 do if f[i] then inc(s); writeln(s); for i:=0 to 100000 do if f[i] then write(i,' '); END.
计数排序
以往的排序算法中,各个元素的位置基于元素直接的比较,这类排序称为比较排序。任意一个比较排序算法在最坏情况下,都需要做Ω(nlgn)次的比较。
而计数排序是基于非排序的思想的,计数排序假设n个输入元素中的每一个都是介于0到k之间的整数。
计数排序的思想是对每一个输入元素x,确定出小于x的元素个数,有了这一信息,就可以把x直接放在它在最终输出数组的位置上,例如,如果有17个元素小于x,则x就是属于第18个输出位置。当几个元素相同是,方案要略作修改。
计数排序是稳定的。
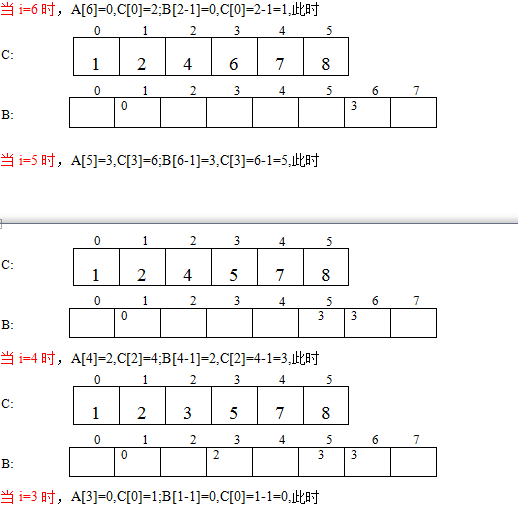
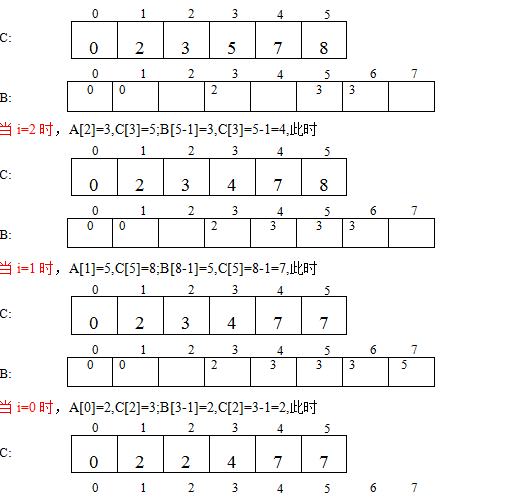
图示
对于数据2 5 3 0 2 3 0 3程序执行的过程如下图所示:
现在有个问题,若必须是0到n的自然数,是不是用途很小?我想了想,其实可以任意整数的,即找出最小的数来,看看与0的距离d,把所有的数同时减去d,划到0到n的范围内,计数排序。到最后待恢复就可以了。