HGOI20180812 (NOIP2018 提高组 Day1 模拟试题)

前缀数组其实就是有序的，那么答案显然是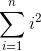     

我们尝试求出通项公式：

证明如下：

因为

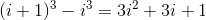
所以：

解之得：

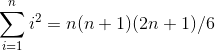
更加通俗的写法如下：

易知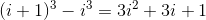 

令

那么，

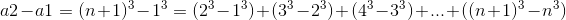
（错位相减）

由易知等式代入得，

所以，

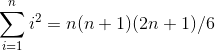
所以程序如下：

# include <bits/stdc++.h>
using namespace std;
char s[1000005] ;
int main()
{
    freopen("absurdity.in","r",stdin);
    freopen("absurdity.out","w",stdout);
    int pig; scanf("%d
",&pig);
    scanf("%s",s);
    int n=strlen(s);
    long long ans=(long long) n*(n+1)*(2*n+1)/6ll;
    printf("%lld
",ans%(1000000007));
    return 0;
}

 

这道题是有点failure的感觉，就是考场上想了个 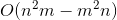  的算法（而且还是错的？！）

我还是讲讲吧，枚举起始位置i往后找m个数字，每次找最优就是后面的l减去前面的L，后面的r被前面的R减去 算出负贡献最小

程序贴下，并不是正确解法（code 39pts）

# include <bits/stdc++.h>
using namespace std;
const int MAXN=1000006;
struct rec{
 int l,r,id;
}a[MAXN];
int n,m,p[MAXN],t[MAXN],ans=0;
bool vis[MAXN];
bool cmp(rec a,rec b)
{
    if (a.l!=b.l) return a.l<b.l;
    else return a.r<b.r;
}
inline int read()  
{
   int x=0,t=1;char ch=getchar();
    if (ch=='-') { t=-1; ch=getchar(); }
    while(ch>'9'||ch<'0') ch=getchar();
    while(ch>='0'&&ch<='9') {
        x=(x<<3)+(x<<1)+(ch^'0');ch=getchar();
    } return x*t;
}
int main()
{
    freopen("failure.in","r",stdin);
    freopen("failure.out","w",stdout);
    int num; scanf("%d",&num);
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++)
     //scanf("%d%d",&a[i].l,&a[i].r)
     a[i].l=read(),a[i].r=read(),a[i].id=i;
    sort(a+1,a+1+n,cmp);
    ans=0;
    memset(p,0,sizeof(p));
    for (int i=1;i<=n-m+1;i++) {
        int L=a[i].l,R=a[i].r;
        t[0]=1;t[1]=a[i].id;
        memset(vis,false,sizeof(vis));
        vis[a[i].id]=true;
        for (int tt=2;tt<=m;tt++) {
           int mm=INT_MAX,k=0;
            for (int j=i+1;j<=n;j++) {
            if (vis[a[j].id]) continue;
             int tot=0;
             if (a[j].l>L) tot+=a[j].l-L;
            if (a[j].r<R) tot+=R-a[j].r;
            if (tot<mm) mm=tot,k=j;  
           }
          vis[a[k].id]=true;
          t[++t[0]]=a[k].id;    
          L=max(L,a[k].l); R=min(R,a[k].r);
        }
        if (R-L>ans) {
            ans=R-L;
            memcpy(p+1,t+1,sizeof(t)-4);
        }
    }
    printf("%d
",ans);
    for (int i=1;i<=m;i++) printf("%d ",p[i]);
    printf("
");
    return 0;
}

讲讲这道题的正解就是用堆来优化算法

 我们知道如果我们枚举的区间是[l₁,r₂][l₂,r₂]......[l_m,r_m]那么显然

=∅ 或者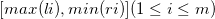

那么我们维护一个有m元素的堆描述我们的答案区间，堆顶元素是指min(r_i)

先按照l排序从1扫到n保证l_i有序那么如果加入一个r_i超过m个元素那么堆顶元素弹出，只要堆里的元素个数恰好为m而且可以更新答案那么就更新答案，随后输出是只要枚举不在了左端点l，右端点r不在[l,r]就是被选中，

包含关系，这里画个图

 正解：

# include <bits/stdc++.h>
using namespace std;
const int MAXN=1000006;
struct qwq{
    int l,r;
};
struct rec{
    qwq val;
    int id;
}a[MAXN];
bool cmp(rec a,rec b)
{
    if (a.val.l!=b.val.l) return a.val.l<b.val.l;
    else return a.val.r<b.val.r;
}
struct cmp1{
    bool operator() (int a,int b) {
        return a>b;
    }
};
priority_queue<int,vector<int>,cmp1>heap;
int ans,n,k;
int main()
{
    int num; scanf("%d",&num);
    scanf("%d%d",&n,&k);
    for (int i=1;i<=n;i++)
     scanf("%d%d",&a[i].val.l,&a[i].val.r),a[i].id=i;
    sort(a+1,a+1+n,cmp);
    int l,r;
    for (int i=1;i<=n;i++) {
        heap.push(a[i].val.r);
        if (heap.size()>k) heap.pop();
        if (heap.size()==k&&heap.top()-a[i].val.l>ans){
            ans=heap.top()-a[i].val.l;
            l=a[i].val.l;r=heap.top();
        }
    }
    printf("%d
",ans);
    if (ans==0) 
        for (int i=1;i<=k;i++) printf("%d ",i); 
    else {
        for (int i=1;i<=n;i++)
         if (a[i].val.l<=l&&a[i].val.r>=r) {
           printf("%d ",a[i].id);
           k--;
           if (k==0) return 0;    
         }  
    }
    return 0;
}

 

 这个题只有std，贴一个

#include<bits/stdc++.h>
using namespace std;
const int MAXS = 1 << 20;
const int P = 1e9 + 7;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
    x = 0; int f = 1;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
    x *= f;
}
template <typename T> void write(T x) {
    if (x < 0) x = -x, putchar('-');
    if (x > 9) write(x / 10);
    putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
    write(x);
    puts("");
}
int n, m, k, cnt[MAXS], bits[MAXS];
int power(int x, int y) {
    if (y == 0) return 1;
    int tmp = power(x, y / 2);
    if (y % 2 == 0) return 1ll * tmp * tmp % P;
    else return 1ll * tmp * tmp % P * x % P;
}
int main() {
    freopen("loneliness.in", "r", stdin);
    freopen("loneliness.out", "w", stdout);
    int num; read(num);
    read(n), read(m), read(k);
    for (int i = 1; i <= m; i++) {
        int x; read(x);
        cnt[x]++;
    }
    int ans = power(m, k), goal = (1 << n) - 1;
    for (int len = 2; len <= (1 << n); len <<= 1) {
        for (int i = 0; i <= goal; i += len)
        for (int j = i, k = i + len / 2; k < i + len; j++, k++)
            cnt[j] += cnt[k];
    }
    for (int i = 1; i <= goal; i++)
        bits[i] = bits[i - (i & -i)] + 1;
    for (int i = 0; i <= goal; i++) {
        if (bits[i] & 1) ans = (ans + power(cnt[i], k)) % P;
        else ans = (ans - power(cnt[i], k) + P) % P;
    }
    writeln(ans);
    return 0;
}