HGOI20180813 (NOIP2018 提高组 Day2 模拟试题)

省常中省选提高Day2 继续

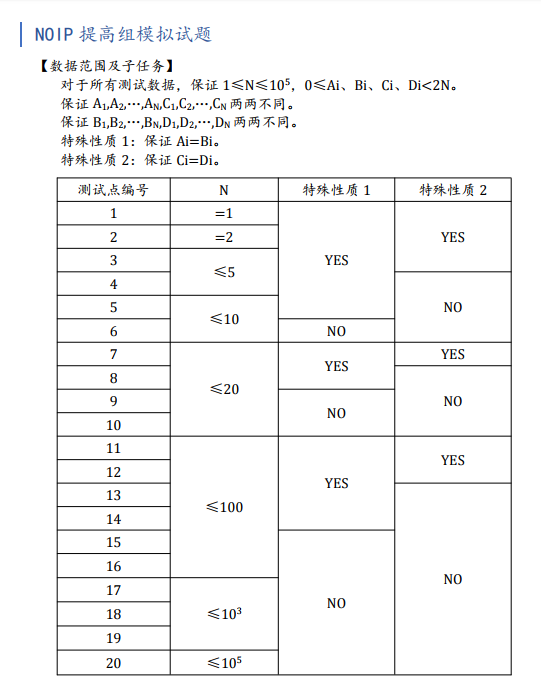
 第一题就考了贪心，正解95pts的贪心策略第一印象是想到的，但是被自己否定掉了qwq，然后打了

不是正解的贪心，样例5没过（可怜）思路如下：先找出每个门对应可以通过的人数是多少，每个人能通过多少门逃走

然后枚举能通过门最少的点优先选，合法门里面可以通过这扇门逃走人数最少的一扇门，这样做（57pts）

贴下代码：

# include <bits/stdc++.h>
using namespace std;
const int MAXN=200010;
struct rec{
    int x,y,cnt;
    bool flag;
};
rec a[MAXN],b[MAXN];
inline bool cmp(rec a,rec b)
{
    if (a.y!=b.y) return a.y<b.y;
    else return a.x<b.x;
}
inline bool cmpa(rec a,rec b)
{
    if (a.cnt!=b.cnt) return a.cnt>b.cnt;
    else if (a.x!=b.x) return a.x<b.x;
    else return a.y<b.y;
}
int main()
{
    //freopen("guide.in","r",stdin);
//    freopen("guide.out","w",stdout);
    int num; scanf("%d",&num);
    int n; scanf("%d",&n);
    for (register int i=1;i<=n;i++) {
        scanf("%d%d",&a[i].x,&a[i].y);
        a[i].x++;a[i].y++;
        a[i].cnt=0;a[i].flag=true;
    }
    for (register int i=1;i<=n;i++) {
        scanf("%d%d",&b[i].x,&b[i].y);
        b[i].x++;b[i].y++;
        b[i].flag=true;
        b[i].cnt=0;
    }
    for (register int i=1;i<=n;i++) {
        for (register int j=1;j<=n;j++) 
         if (b[j].x>=a[i].x&&b[j].y>=a[i].y) b[j].cnt++,a[i].cnt++;
    }
    int ans=0;
    int yy=0;
    for (register int i=1;i<=n;i++) {
        int maxx=0,minn=INT_MAX,p=-1,w;
        for (register int j=1;j<=n;j++)
            if (a[j].flag) {
                if (a[j].cnt<=minn) {
                    minn=a[j].cnt; w=j; 
                }else if (a[j].cnt==minn&&a[j].x>a[w].x){
                    minn=a[j].cnt; w=j; 
                }else if (a[j].cnt==minn&&a[j].x==a[w].x&&a[j].y>a[w].x){
                    minn=a[j].cnt; w=j; 
                }
            }
        a[w].flag=false;
        minn=INT_MAX;
        for (register int j=1;j<=n;j++) 
         if (b[j].flag&&b[j].x>=a[w].x&&b[j].y>=a[w].x&&b[j].cnt<=minn)
         if (b[j].cnt<minn){
             p=j; minn=b[j].cnt;
         } else if (b[j].x>b[p].x) {
             p=j; minn=b[j].cnt;
         } else if (b[j].x==b[p].x&&b[j].y>b[p].x) {
             p=j; minn=b[j].cnt;
         }
         if (p==-1) continue;
         b[p].flag=false; ans++;
         for (int j=1;j<=n;j++) if (a[j].x<=b[p].x&&a[j].y<=b[p].y) a[j].cnt--;
         for (int j=1;j<=n;j++) if (b[j].x<=a[w].x&&b[j].y<=a[w].y) b[j].cnt--;
    }
    printf("%d
",ans);
    return 0;
}

正解是什么呢？

其实出奇的简单，从左到右扫每一个门，然后找这个门前面合法的y坐标最小的人。这样可以过95pts。

但是这里开了O2优化所以我们考虑stl优化O（n²）的初始化维护：set

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 200005;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
    x = 0; int f = 1;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
    x *= f;
}
template <typename T> void write(T x) {
    if (x < 0) x = -x, putchar('-');
    if (x > 9) write(x / 10);
    putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
    write(x);
    puts("");
}
set <int> st;
bool type[MAXN]; int pos[MAXN];
int main() {
    freopen("guide.in", "r", stdin);
    freopen("guide.out", "w", stdout);
    int num; read(num);
    int n; read(n);
    for (int i = 1; i <= n; i++) {
        int x, y; read(x), read(y);
        type[x] = true, pos[x] = y;//type[x]表示x坐标的这个位置是人（true）还是人（false）
    }
    for (int i = 1; i <= n; i++) {
        int x, y; read(x), read(y);
        type[x] = false, pos[x] = y;
    }
    int ans = 0;
    for (int i = 0; i < 2 * n; i++) {
        if (type[i]) st.insert(pos[i]);//如果x坐标这个位置是人，那么塞入set（待门来找）
        else {
            set <int> :: iterator tmp = st.lower_bound(pos[i]);//tmp指向这个门前面下面离这个门最近的人之后的那个位置
            if (tmp == st.begin()) continue;//如果没找到就continue
            tmp--; ans++; //累加答案
            st.erase(tmp);//注意tmp是指这个门前面下面离这个门最近的人之后的那个位置而不是人的位置刚好比人的位置多1，所以tmp--才是指向那个人
        }
    }
    writeln(ans);
    return 0;
}

 看数据范围这道题是dfs，需要注意这样一个性质：

不管怎么换行中的数字是不会发生除了顺序的变化的，那么我们就暴力找出每一次交换，看看个数是否相同，如果相同就是合法

如果不同就是不合法就不对应的，这是可行性剪枝。（首先你要保证每行的个数一样，才能最终判断）

既然暴力判断交换那么就不用记录状态了，直接回溯暴力判断是否是中心对称即可

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 15;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
    x = 0; int f = 1;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
    x *= f;
}
template <typename T> void write(T x) {
    if (x < 0) x = -x, putchar('-');
    if (x > 9) write(x / 10);
    putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
    write(x);
    puts("");
}
int n, m;
char mp[MAXN][MAXN];
int rnum[MAXN], cnum[MAXN];
bool visrow[MAXN], viscol[MAXN], solved;
bool row[MAXN][MAXN], col[MAXN][MAXN];
void check() {
    for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
        if (mp[rnum[i]][cnum[j]] != mp[rnum[n - i + 1]][cnum[m - j + 1]]) return;
    printf("YES
");
    solved = true;
}
void workc(int pos, int type) {
    if (solved) return;
    if (pos == 0) {
        check();
        return;
    }
    if (type) {
        for (int i = 1; i <= m; i++) {
            viscol[i] = true;
            cnum[pos] = i;
            workc(pos - 1, 0);
            viscol[i] = false;
        }
    } else {
        for (int i = 1; i <= m; i++) {
            if (viscol[i]) continue;
            for (int j = i + 1; j <= m; j++)
                if (!viscol[j] && col[i][j]) {
                    viscol[i] = true;
                    viscol[j] = true;
                    cnum[pos] = i;
                    cnum[m + 1 - pos] = j;
                    workc(pos - 1, 0);
                    viscol[i] = false;
                    viscol[j] = false;
                }
            return;
        }
    }
}
void workr(int pos, int type) {
    if (solved) return;
    if (pos == 0) {
        workc((m + 1) / 2, m & 1);
        return;
    }
    if (type) {
        for (int i = 1; i <= n; i++) {
            visrow[i] = true;
            rnum[pos] = i;
            workr(pos - 1, 0);
            visrow[i] = false;
        }
    } else {
        for (int i = 1; i <= n; i++) {
            if (visrow[i]) continue;
            for (int j = i + 1; j <= n; j++)
                if (!visrow[j] && row[i][j]) {
                    visrow[i] = true;
                    visrow[j] = true;
                    rnum[pos] = i;
                    rnum[n + 1 - pos] = j;
                    workr(pos - 1, 0);
                    visrow[i] = false;
                    visrow[j] = false;
                }
            return;
        }
    }
}
int main() {
    freopen("fragment.in", "r", stdin);
    freopen("fragment.out", "w", stdout);
    int T, num; read(num), read(T);
    while (T--) {
        read(n), read(m);
        for (int i = 1; i <= n; i++)
            scanf("%s", mp[i] + 1);
        for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) {
            static char x[MAXN], y[MAXN];
            for (int k = 1; k <= m; k++) {
                x[k] = mp[i][k];
                y[k] = mp[j][k];
            }
            sort(x + 1, x + m + 1);
            sort(y + 1, y + m + 1);
            row[i][j] = true;
            for (int k = 1; k <= m; k++)
                if (x[k] != y[k]) row[i][j] = false;
        }
        for (int i = 1; i <= m; i++)
        for (int j = 1; j <= m; j++) {
            static char x[MAXN], y[MAXN];
            for (int k = 1; k <= n; k++) {
                x[k] = mp[k][i];
                y[k] = mp[k][j];
            }
            sort(x + 1, x + n + 1);
            sort(y + 1, y + n + 1);
            col[i][j] = true;
            for (int k = 1; k <= n; k++)
                if (x[k] != y[k]) col[i][j] = false;
        }
        solved = false;
        workr((n + 1) / 2, n & 1);
        if (!solved) printf("NO
");
    }
    return 0;
}

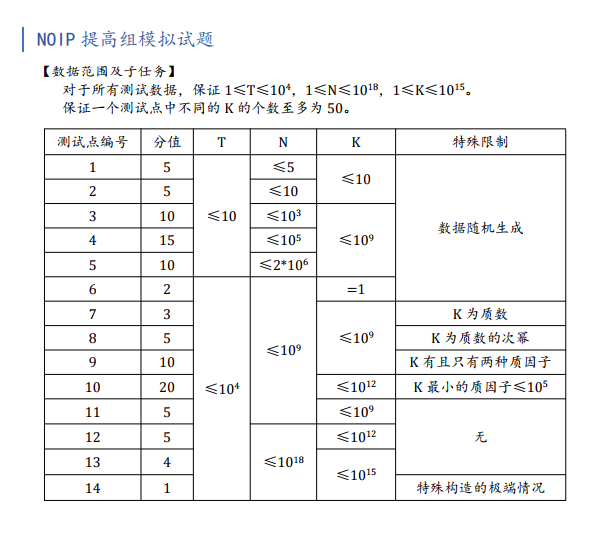
由于在K天之后必须所有的旅者都要回到他的家乡所以这n个人的初始序列按照题意模拟必须要是多个环，

且这些环的长度必须是k的质因数，那么这个问题就转变为对K进行质因数分解求出的所有质因数的多重集求和恰为n是否合法

我们现在考虑这个问题，

显然输入的K可能会有重复所以我们并不用每次对K都分解质因数，所以我们用memk[i]记录当前都多少不同种类的K ，q为当前数目

设当前是在memk数组中的第pos个K是当前的K那么p[pos][ ]为mem[pos]的质因数，个数记为cnt[pos]

讲了一大坨就是这个程序：

        read(n), read(k);//读入n k
        int pos = 0; //找之前算过的k
        for (int i = 1; i <= q; i++)
            if (memk[i] == k) pos = i; //找K
        if (pos == 0) {//没找到qwq
            pos = ++q; 
            memk[q] = k;
            long long tmp = k; //分解质因数tmp=k
            for (int i = 1; 1ll * prime[i] * prime[i] <= tmp; i++)
                if (tmp % prime[i] == 0) {
                    p[pos][++cnt[pos]] = prime[i];
                    while (tmp % prime[i] == 0) tmp /= prime[i];
                }
            if (tmp != 1) p[pos][++cnt[pos]] = tmp;//分解质因数

我们来讨论几种简单的情况

cnt[pos]=1那么如果这个仅存的质因数被n整除那么久不行，否则行

    bool flg = false;
        for (int i = 1; i <= cnt[pos]; i++)//依次检测
            if (n % p[pos][i] == 0) {//行，那么就是true
                printf("YES
");
                flg = true;
                break;
            }
        if (flg) continue; 
        if (cnt[pos] <= 1) {//否则就是false
            printf("NO
");
            continue;
        }

cnt[pos]=2的情况就是ax+by=n求是否存在正数解(a,b)那么就是ex_gcd

这里是ex_gcd的板子（求ax+by=gcd(a,b)求（x，y）的值）

void exgcd(long long a, long long b, long long &x, long long &y) {
    if (b == 0) {
        x = 1;
        y = 0;
        return;
    }
    long long q = a / b, r = a % b;
    exgcd(b, r, y, x);
    y -= q * x;
}

考虑这样一个问题 已知xp1+yp2=gcd(p1,p2)=1求xp1+yp2=n的解

令x‘p1+y'p2=n成立，xp1+yp2=1成立

那么就有n（xp1+yp2）=n 所以nxp1+nyp2=n;

所以x'=nx,y'=ny，最小化y'（但是保证大于0）才可能让x’尽可能大直到x>0；

根据定理可知y‘最小为ny%p1，

证明的话就是那 一直从y中拿p1到不能拿为止这个时候就是y-[y/p1]*p1就是就是y%p1，加个n就是ny%p1

所以这里的p1放在全局看就是第一个质因数，p2就是第二个质因数

程序的话就是这样：

        if (cnt[pos] == 2) {
            long long x = 0, y = 0;
            exgcd(p[pos][1], p[pos][2], x, y);
            y = (y % p[pos][1] + p[pos][1]) % p[pos][1];//求出最小的y
            long long tmp = y * (n % p[pos][1]) % p[pos][1] * p[pos][2]; //求出最大的x
            if (tmp <= n) printf("YES
"); //若最大的n不大于n就是true
            else printf("NO
");//否则是false
            continue;
        }

cnt[pos]>3怎办？

我们设dist[pos][i]表示第pos个数用所有除第一个质因子外乱加求和（带自定义权求和）得到的sum值%i最小是多少

我们考虑这样一个问题

n=xp1+y（x是p1的系数y是乱加求和sum和）显然要想n分解成立那么y必须要不大于n%p1，解释的话就是如果多了那么不用加y直接进加x就行了

这样我们可以用一个形如堆优化dijkstra算法就行求出最小的sum%i的值

    if (cnt[pos] >= 3) {
                for (int i = 0; i < p[pos][1]; i++)
                    dist[pos][i] = INF;
                static priority_queue <info> Heap;
                dist[pos][0] = 0; Heap.push((info) {0, 0});
                //info有两个值dist和home，dist表示乱加数值的和，home表示%i后的余数
                static bool vis[MAXN];
                memset(vis, false, sizeof(vis));
                while (!Heap.empty()) {
                    while (!Heap.empty() && vis[Heap.top().home]) Heap.pop();
                    if (Heap.empty()) break;
                    info tmp = Heap.top(); Heap.pop();
                    for (int i = 2; i <= cnt[pos]; i++) {
                        int dest = (tmp.home + p[pos][i]) % p[pos][1]; //乱加
                        if (dist[pos][dest] > tmp.dist + p[pos][i]) {
                            dist[pos][dest] = tmp.dist + p[pos][i];
                            Heap.push((info) {dist[pos][dest], dest});
                        }
                    }
                }
            }
        }

判断的话就是这样：

    int tmp = n % p[pos][1];//就是y
        if (dist[pos][tmp] <= n) printf("YES
");//有乱加的sum%y<=n就一定可以
        else printf("NO
");

那么std如下：

#include<bits/stdc++.h>
using namespace std;
const int MAXQ = 55;
const int MAXLOG = 64;
const int MAXN = 100005;
const int MAXP = 2e6 + 5;
const int MAXV = 3.2e7 + 5;
const long long INF = 4e18;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
    x = 0; int f = 1;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
    x *= f;
}
template <typename T> void write(T x) {
    if (x < 0) x = -x, putchar('-');
    if (x > 9) write(x / 10);
    putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
    write(x);
    puts("");
}
int q; long long memk[MAXQ];
int tot, prime[MAXP], f[MAXV];
int cnt[MAXQ]; long long p[MAXQ][MAXLOG];
long long dist[MAXQ][MAXN];
struct info {long long dist; int home; };
bool operator < (info a, info b) {
    return a.dist > b.dist;
}
void exgcd(long long a, long long b, long long &x, long long &y) {
    if (b == 0) {
        x = 1;
        y = 0;
        return;
    }
    long long q = a / b, r = a % b;
    exgcd(b, r, y, x);
    y -= q * x;
}
int main() {
    freopen("fantasy.in", "r", stdin);
    freopen("fantasy.out", "w", stdout);
    int num; read(num);
    for (int i = 2; i < MAXV; i++) {
        if (f[i] == 0) prime[++tot] = f[i] = i;
        for (int j = 1; j <= tot && prime[j] <= f[i]; j++) {
            int tmp = prime[j] * i;
            if (tmp >= MAXV) break;
            f[tmp] = prime[j];
        }
    }
    int T; read(T);
    while (T--) {
        long long n, k;
        read(n), read(k);
        int pos = 0;
        for (int i = 1; i <= q; i++)
            if (memk[i] == k) pos = i;
        if (pos == 0) {
            pos = ++q;
            memk[q] = k;
            long long tmp = k;
            for (int i = 1; 1ll * prime[i] * prime[i] <= tmp; i++)
                if (tmp % prime[i] == 0) {
                    p[pos][++cnt[pos]] = prime[i];
                    while (tmp % prime[i] == 0) tmp /= prime[i];
                }
            if (tmp != 1) p[pos][++cnt[pos]] = tmp;
            if (cnt[pos] >= 3) {
                for (int i = 0; i < p[pos][1]; i++)
                    dist[pos][i] = INF;
                static priority_queue <info> Heap;
                dist[pos][0] = 0; Heap.push((info) {0, 0});
                static bool vis[MAXN];
                memset(vis, false, sizeof(vis));
                while (!Heap.empty()) {
                    while (!Heap.empty() && vis[Heap.top().home]) Heap.pop();
                    if (Heap.empty()) break;
                    info tmp = Heap.top(); Heap.pop();
                    for (int i = 2; i <= cnt[pos]; i++) {
                        int dest = (tmp.home + p[pos][i]) % p[pos][1];
                        if (dist[pos][dest] > tmp.dist + p[pos][i]) {
                            dist[pos][dest] = tmp.dist + p[pos][i];
                            Heap.push((info) {dist[pos][dest], dest});
                        }
                    }
                }
            }
        }
        bool flg = false;
        for (int i = 1; i <= cnt[pos]; i++)
            if (n % p[pos][i] == 0) {
                printf("YES
");
                flg = true;
                break;
            }
        if (flg) continue;
        if (cnt[pos] <= 1) {
            printf("NO
");
            continue;
        }
        if (cnt[pos] == 2) {
            long long x = 0, y = 0;
            exgcd(p[pos][1], p[pos][2], x, y);
            y = (y % p[pos][1] + p[pos][1]) % p[pos][1];
            long long tmp = y * (n % p[pos][1]) % p[pos][1] * p[pos][2];
            if (tmp <= n) printf("YES
");
            else printf("NO
");
            continue;
        }
        int tmp = n % p[pos][1];
        if (dist[pos][tmp] <= n) printf("YES
");
        else printf("NO
");
    }
    return 0;
}