本文版权归ljh2000和博客园共有,欢迎转载,但须保留此声明,并给出原文链接,谢谢合作。
本文作者:ljh2000
作者博客:http://www.cnblogs.com/ljh2000-jump/
转载请注明出处,侵权必究,保留最终解释权!
Description
During the programming classes Vasya was assigned a difficult problem. However, he doesn't know how to code and was unable to find the solution in the Internet, so he asks you to help.
You are given a sequence a, consisting of n distinct integers, that is used to construct the binary search tree. Below is the formal description of the construction process.
- First element a1 becomes the root of the tree.
- Elements a2, a3, ..., an are added one by one. To add element ai one needs to traverse the tree starting from the root and using the following rules:
- The pointer to the current node is set to the root.
- If ai is greater than the value in the current node, then its right child becomes the current node. Otherwise, the left child of the current node becomes the new current node.
- If at some point there is no required child, the new node is created, it is assigned value ai and becomes the corresponding child of the current node.
The first line of the input contains a single integer n (2 ≤ n ≤ 100 000) — the length of the sequence a.
The second line contains n distinct integers ai (1 ≤ ai ≤ 109) — the sequence a itself.
Output n - 1 integers. For all i > 1 print the value written in the node that is the parent of the node with value ai in it.
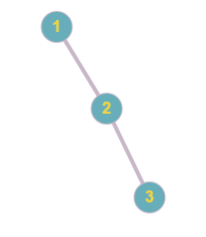
3
1 2 3
1 2
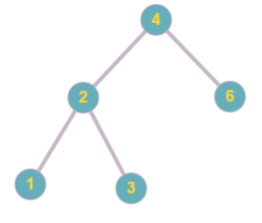
5
4 2 3 1 6
4 2 2 4
Picture below represents the tree obtained in the first sample.
Picture below represents the tree obtained in the second sample.
正解:set维护平衡树
解题报告:
以前做过的题,只需维护前驱后继即可。
ps:特判两边相等的情况。
//It is made by ljh2000
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <string>
#include <complex>
using namespace std;
typedef long long LL;
const int inf = (1<<30);
const int MAXN = 200011;
int n,deep[MAXN],father[MAXN],ql,qr,nowl,nowr,val[MAXN];
set<int>bst;
map<int,int>mp;
inline int getint(){
int w=0,q=0; char c=getchar(); while((c<'0'||c>'9') && c!='-') c=getchar();
if(c=='-') q=1,c=getchar(); while (c>='0'&&c<='9') w=w*10+c-'0',c=getchar(); return q?-w:w;
}
inline void work(){
n=getint(); int x; bst.insert(inf); bst.insert(-inf);
val[1]=x=getint(); bst.insert(x); mp[x]=1;
for(int i=2;i<=n;i++) {
x=getint(); val[i]=x;
ql=*--bst.lower_bound(x);
qr=*bst.lower_bound(x);
if(ql==(-inf)) father[i]=mp[qr];
else if(qr==inf) father[i]=mp[ql];
else{
if(nowl<nowr) father[i]=mp[ql];
else if(nowl>nowr) father[i]=mp[qr];
else{
int ll=mp[ql],rr=mp[qr];
if(ll>rr) father[i]=ll;
else father[i]=rr;
}
}
deep[i]=deep[father[i]]+1;
bst.insert(x); mp[x]=i;
//printf("%d %d
",father[i],deep[i]);
printf("%d ",val[father[i]]);
}
}
int main()
{
work();
return 0;
}