递归函数的使用

一，概念

        直接或间接地调用自身的算法称为递归算法。

          用函数自身给出定义的函数称为递归函数。

二，实例

      实例1：阶乘函数。

         通过分析可知，要求一个数的阶乘，只要知道它前一位数的阶乘便可求出。 即：n!=n*(n-1)!

  而要求前一位数的阶乘，只要知道它前前一位数的阶乘即可，即：(n-1)!=(n-1)*(n-2)!,因为每次

  计算的方式都相同，所以考虑用递归的方式求解。

        递归关系：f(n)=n*f(n-1)

        递归结束条件：n=1  (因为我们很容易知道1阶乘是1，因此求解其他数的阶乘时，可从1的阶乘开始求起） 

      代码实现：

import java.util.*;
public class HW8 {
    public static void main(String[] args) {
        Scanner in=new Scanner(System.in);
        System.out.println("请输入所要求的数值：");
        int n=in.nextInt();     //输入所要遍历的数
        int number=funtion(n);
        System.out.println(n+"的阶乘为："+number);

    }

    /**
     * 求第n个数的阶乘！！！
     * @param n 所要求的数的值
     * @return  所要求的数的阶乘
     * 递归函数结束条件：n<=1
     */
    private static int funtion(int n) {
        if(n==1)      //递归函数的结束条件
        {
            return 1;
        }else{
            return n*funtion(n-1);
        }

    }
}

 运行结果：

实例2：

    用递归判断一个数组是否是一个递增序列的数组。

 代码实现：

import java.util.*;
public class HW8 {
    public static void main(String[] args) {

        int[] arr = new int[20]; //定义一个可存放20个元素的数组
        Random rd = new Random();
        for (int i = 0; i < arr.length; i++)     //对数组随机赋值
        {
            arr[i] = rd.nextInt(50) + 1; //范围：1-50
        }
        System.out.println(Arrays.toString(arr));  //对arr数组进行打印
        Arrays.sort(arr);                          //对arr数组进行排序
        System.out.println(Arrays.toString(arr));  //对排完序的数组进行打印
        boolean flag = funtion(arr);
        if (flag) {
            System.out.println("该数组是一个有序数组！！！");
        } else {
            System.out.println("无序数组！！！");
        }
    }

    /**
     * 求该数组是否为一个增序数组
     *
     * @param arr 所要验证的数组
     * @return 增序：true    无或减序：false
     */
    private static boolean funtion(int[] arr) {
        int index = 0;
        return funtion2(arr, index);    //因为对数组进行递归时，要让数组的长度不断减小
                                        //所以要借助下标
    }

    private static boolean funtion2(int[] arr, int index) {
        if (index == arr.length - 1) {        //如果数组小标等于数组长度-1，则说明对数组元素遍历完了
            return true;                      //且中途没有出现乱序，此时返回true
        } else {              
            if (arr[index] >arr[index + 1]) {    //出现非增序列，直接返回false
                return false;
            } else {
                return funtion2(arr, index+1);   //若前面排序正常，则调用方法继续检测后面的数组元素
            }                                           //此时下标+1
        }


    }

}

 运行结果:

实例3：

      （ 用递归求解字符串中，字符的个数。）

      通过分析可知，要求解一个字符串str的长度值，首先应知道str.length()-1的值，而要知道str.length()-1的值，

则要先知道str.length()-2的值，由此不断的递归，可知，知道str-（str.length()-1）的值，即：1，则可求出整个

字符串的长度。

     递归关系：f(n)=f(n-1)+1

     递归结束条件：index=str.length()-1;   (当下标移动到最后一个下标时，则说明整个字符串已被统计完）

代码实现：

import java.util.*;
public class HW8 {
    public static void main(String[] args) {
        Scanner in=new Scanner(System.in);
        System.out.println("请输入一个字符串：");
        String str=in.nextLine();
        int number=count(str);
        System.out.println("统计该字符串的长度为："+number);

    }

    /**
     * 求解字符串中，字符的个数。
     * @param str 所要求解的字符串
     * @return    所统计的字符个数
     */
    private static int count(String str) {  //将所要求解的字符串传给该方法
        int index=0;                   //因为要统计字符串的个数，必须要借助下标
        return count2(str,index);  //所以在次调用方法count2
    }

    private static int count2(String str, int index) {  
        if(index==str.length()-1)     //当下标移动到最后一个位置时，则统计完成
        {
            return 1;          开始返回，实现“归”
        }else{
            return count2(str,index+1)+1;  //当下标还没移动到最后一个位置时，该位置的字符串长度为：（比它少一位的字符串段长度）+1
        }
    }
}

运行结果：

实例4：（用递归实现有序数组的二分搜索)

           通过分析可知，要对一个数组进行二分搜索，首先要求解出该数组中间值，将所查找的数与该

中间数进行比较，若相等则返回该中间值下标。若小于则将middle-1的值赋给right，将范围进行缩减，

然后又开始执行上述操作。若大于则将middle+1的值赋给left，将范围进行缩减，然后又开始执行上述操作。

import java.util.*;
public class HW8 {
    public static void main(String[] args) {
        int[] arr = new int[10]; //定义一个可存放10个元素的数组
        Scanner in=new Scanner(System.in);
        Random rd = new Random();
        for (int i = 0; i < arr.length; i++)     //对数组随机赋值
        {
            arr[i] = rd.nextInt(50) + 1; //范围：1-50
        }
        System.out.println(Arrays.toString(arr));  //对arr数组进行打印
        Arrays.sort(arr);                          //对arr数组进行排序
        System.out.println(Arrays.toString(arr));  //对排完序的数组进行打印
        System.out.println("请输入所要查找的数：");
        int number=in.nextInt();
        int index=binarySearch(arr,number,0,arr.length-1);
        if (index==-1) {
            System.out.println("没有查找到该数！！！");
        } else {
            System.out.println("所要查找的数为："+arr[index]+"该数的下标为"+index);
        }
    }

    /**
     *
     *用递归实现有序数组的二分搜索
     * @param arr 进行搜索的数组
     * @number  要查找的数
     * @left     开始下标
     * @right    结束下标
     * @return     若找到返回下标，否则返回-1
     *    递归结束条件：left>right
     */
    private static int binarySearch(int[] arr,int number,int left,int right) {
        int middle=(left+right)/2;
        if(left>right)       
        {
            return -1;
        }else{
            if(arr[middle]==number)
            {
                return middle;
            }else if(arr[middle]>number)
            {
                //right=middle-1;    为简缩代码一般将该语句放在下次调用方法的赋值中
                return binarySearch(arr,number,left,middle-1);
            }else{
                //left=middle+1;
                return binarySearch(arr,number,middle+1,right);
            }

        }

    }
}

运行结果：

 递归调用过程：

实例5：

用递归解决下面问题：

                                  有三种面值的硬币，分别是1分，2分，5分

                                   现在给出一个价值，例如价值为11，问组成该价值至少需要的硬币数量是多少？？？

import java.util.*;
public class HW8 {
    public static void main(String[] args) {
        Scanner in=new Scanner(System.in);
        System.out.println("请输入硬币的价值：");
        int value=in.nextInt();
        int count=fountion(value);
        System.out.println("至少需要的硬币数量："+count);
    }

    private static int fountion(int value) {
        if(value>=5)
        {
            return 1+fountion(value-5);
        }else if(value<5&&value>=2)
        {
            return 1+fountion(value-2);
        }else if(value>=1&&value<2)
        {
            return 1;
        }else
22             {
23              return 0;
24             }
    }
}

价值      至少需要的硬币数量

    1              1

    2              1

    3              2

   4                2

   5                1

   6                2

  ~                ~

---

    通过观察可知，当硬币数为1，2，5时只需一枚硬币。当硬币数为3，4时，只需2枚硬币数。

当大于5时，用价值-5，继续上述循环。。。。

import java.util.*;
public class HW8 {
    public static void main(String[] args) {
        Scanner in=new Scanner(System.in);
        System.out.println("请输入硬币的价值：");
        int value=in.nextInt();
        int count=fountion(value);
        System.out.println("至少需要的硬币数量："+count);
    }

    private static int fountion(int value) {
        if(value==1||value==2||value==5)
        {
            return 1;
        }else if(value>2&&value<5)
        {
            return 2;
        }
        return 1+fountion(value-5);

    }
}

 

实例6:    (汉诺塔问题）

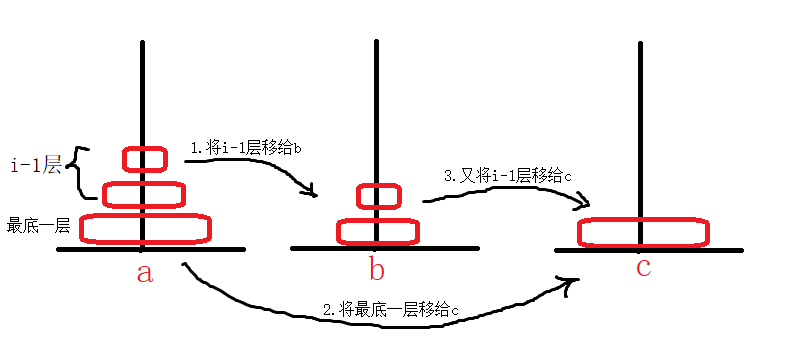
       通过分析可知，对于有n层的汉诺塔问题，可将其看作成两层（上面的i-1层 ，最底1层）来操作，

首先将上面的i-1层从a借助c移动到b，然后将最底下的一层从a直接移到c，最后将b上的i-1层借助a移动

到c。而对于如何将i-1层从a移动到b的问题与上述过程类似，所以调用递归来解决。

public class HW8 {
    public static void main(String[] args) {
    Scanner in=new Scanner(System.in);
        System.out.println("请输入汉诺塔的层数：");
        int number=in.nextInt();
        hanoi(number,'a','b','c');
    }

    /**
     * 求出有n层汉诺塔时的移动过程
     * @param i   汉诺塔的层数
     * @param a     起始柱
     * @param b     辅助柱
     * @param c     目标柱
     *              将n层的塔假设成两层，（1层，n-1层）
     */
    private static void hanoi(int i, char a, char b, char c) {
        if(i>1)
        {
            hanoi(i-1,a,c,b);                  //当为两个时，先将上面的从a移给b (a->b)   [此时有很多，所以要借助b]
            System.out.println(a+"->"+c);    //然后将底下的从a移给c (a->c)       [因为此时a上只剩一个，直接移动]
            hanoi(i-1,b,a,c);              //然后将b的在移给c   (b->c)       [此时有很多，所以要借助b]
                                               //…………此时就完成了一次的移动过程…………//
        }else{
            System.out.println(a+"->"+c);   //当为一个时，直接将a上的移给c  (a->c)
        }

    }
}