树，二叉树

树

一、树的定义

1，树Tree是n(n >= 0) 个结点的有限集， n = 0时 称为空树 。

        在任意一棵非空的树中：

　　（1）有且仅有一个特定的根结点

　　（2）当n>1时，其余节点可分为m（m > 0）个互不相交的有限集T1,T2,.....,Tm，其中每一个集合又是一棵树，并且称为根的子树。

        如下图所示

       

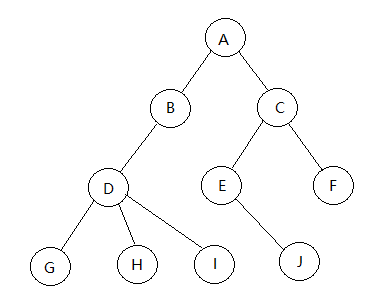
2，结点

       （1）结点包含一个数据元素以及若干指向其子树的分支。

　　（2）结点拥有的子树数量称为结点的度

　　（3）度为0的结点称为叶节点或终端节点

　　（4）度不为0的结点称为非终端结点或分支结点

　　（5）一棵树的度是树内各结点的度的最大值

3，结点间的关系

　　结点的子树的根称为该结点的孩子，该结点称为孩子的双亲。同一个双亲的孩子之间互称兄弟。

       结点的祖先是从根到该结点所经分支上的所有结点。反之，以某结点为根的子树中的任一结点都成为该结点的子孙。

4，树的特性

　　1.节点的度：一个节点含有的子树的个数称为该节点的度。

　　2.树的度：一棵树中，最大的结点的度称为树的度。（注意度与高度是不同的）

　　3.叶节点或终端结点：度为零的结点。

　　4.非终端节点或分支节点：度不为零的结点。

　　5.父亲结点或父结点：若一个结点含有子节点，则这个结点称为其子节点的父节点。

　　6.孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；

　　7.兄弟节点：具有相同父节点的节点互称为兄弟节点。

　　8.深度：对于任意节点n，n的深度为从根到n的唯一路径长，根的深度为0。

　　9.高度：对于任意节点n，n的高度为从n到那一片树叶的最长路径长，所有树叶的高度为0；

　　10.堂兄弟节点：父节点在同一层的节点互为堂兄弟节点。

　　11.节点的祖先：从根到该节点所经分支上的所有节点。

　　12.子孙：以某节点为根的子树中任一节点都称为该节点的子孙。

　　13.森林：由m课互不相交的树的集合称为森林。

　　14.树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树，反之是有序树。

二叉树

二，二叉树 

         二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

        二叉树有如下特性：

1、每个结点都包含一个元素以及n个子树，这里0≤n≤2。
2、左子树和右子树是有顺序的，次序不能任意颠倒。左子树的值要小于父结点，右子树的值要大于父结点。

　　二叉树的特点：

　　1，若二叉树的层数从0开始，则在二叉树的第 i 层最多有2^i个结点。

　　2，高度为K的二叉树最多有2^(k+1)-1个结点。

1.定义：满二叉树：每层的结点数都达到最大值，则这个二叉树就是满二叉树。

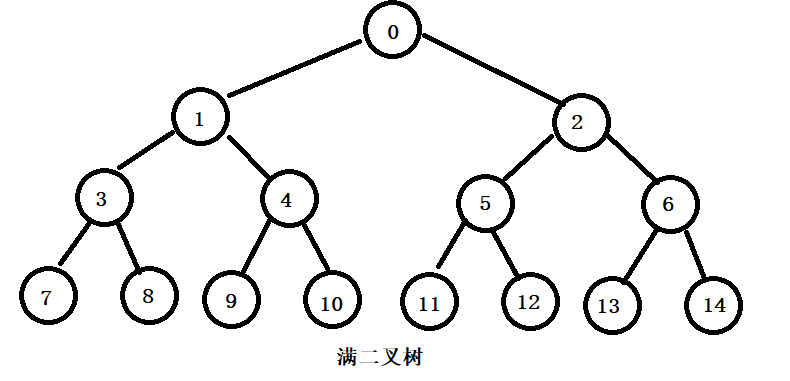
 2.定义：完全二叉树：若设二叉树的高度为h，则共有h+1层。除第h层外，其他各层的结点都达到了最大个数，第h层从右向左连续缺若干结点，这就是完全二叉树。

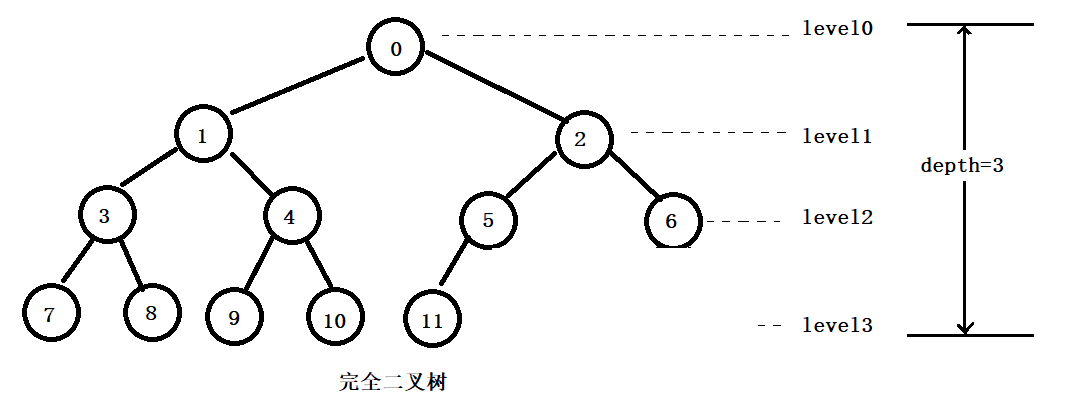
3.二叉树的遍历

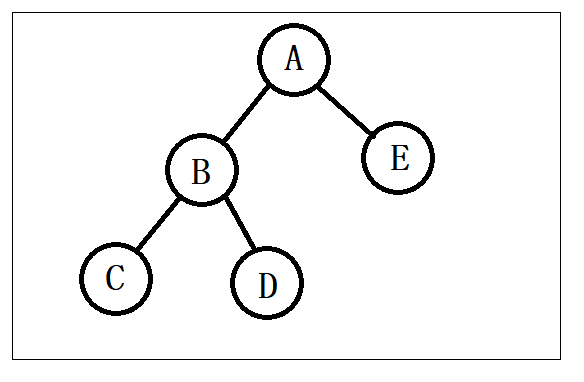
以上述图为例来叙述二叉树的遍历过程：

中序遍历规则：

  若二叉树为空，则结束；

  否则，中序遍历左子树，访问根节点，中序遍历右子树。

  简单理解就是，当二叉树为空时，则结束；否则遍历根节点的左子树，如果左子树不为空（也就是n!=0），则继续遍历左子树的左子树，如果此时这个左子树为空则返回该节点，然后遍历该节点的根节点，接着遍历右子树，便利完后遍历该根节点的根节点。

  中序遍历上面二叉树：CBDAE

前序遍历规则：

  若二叉树为空，则结束；

  否则，访问根节点，前序遍历左子树，前序遍历右子树。

  前序遍历上面二叉树：ABCDE

后序遍历规则：

  若二叉树为空，则结束；

  否则，后序遍历左子树，后序遍历右子树，访问根节点。

  后序遍历上面二叉树：CDBEA

 为了加深理解，下面在举一个例子：(其中深色的框框表示给子树为空子树)

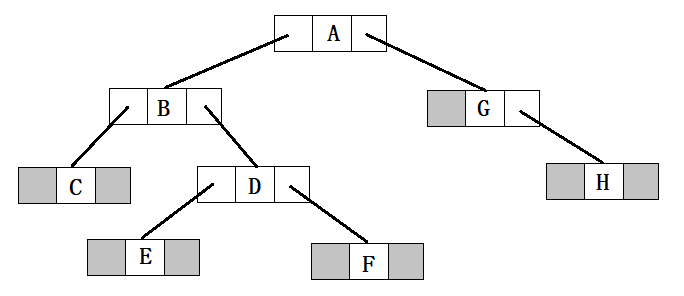
中序遍历：CBEDFAGH

前序遍历：ABCDEFGH

后序遍历：CEFDBHGA

4，代码实现前中后序的遍历。

//创建节点类
class TreeNode{
    public TreeNode LeftNode; //左孩子
    public TreeNode RightNode; //右孩子
    public char data; //该节点的数据值
    public TreeNode(char data){
        this.data=data;
    }
    public void setLeftNode(TreeNode leftNode) {
        LeftNode = leftNode;
    }
    public void setRightNode(TreeNode rightNode) {
        RightNode = rightNode;
    }
}
class Int{
    private int index=0;
    public void setIndex(int index) {
        this.index = index;
    }
    public int getIndex() {
        return index;
    }
    public int Inc(){//实现自增
        return ++index;
    }
}
public class BinaryTree {
    //创建一个二叉树，为了方便实现，其中的空节点是由#代替的,例如：A B C # # D # E # #
    public TreeNode CreateTree(String Treestr,Int i){
        TreeNode s=null;
        if(Treestr.charAt(i.getIndex())!='#'){//等于‘#’说明该节点为空，直接返回底下null
            //不为空，则创建该节点，并创建它的左子树和右子树
             s=new TreeNode(Treestr.charAt(i.getIndex()));
             i.Inc();//i++
             s.setLeftNode( CreateTree(Treestr,i));//创建左子树
             i.Inc();//i++
             s.setRightNode( CreateTree(Treestr,i));//创建右子树
        }
        return s;
    }
    //对二叉树进行中序遍历id
    public void MidOrder(TreeNode tnode){
        if(tnode!=null){//如果该节点不为null
            MidOrder(tnode.LeftNode);//先遍历该节点左子树，如果该左子树的节点还有左子树，就继续遍历，直至为空
            System.out.print(tnode.data);//遍历完左子树，在访问根结点
            MidOrder(tnode.RightNode);
        }
    }
    //对二叉树进行先序遍历
    public void PreOrder(TreeNode tnode){
        if(tnode!=null){//如果该节点不为null
            System.out.print(tnode.data);//先访问根节点
            PreOrder(tnode.LeftNode);//再遍历该节点左子树，如果该左子树的节点还有左子树，就继续遍历，直至为空
            PreOrder(tnode.RightNode);
        }
    }
    //对二叉树进行后序遍历
    public void AftOrder(TreeNode tnode){
        if(tnode!=null){//如果该节点不为null
            AftOrder(tnode.LeftNode);//先遍历该节点左子树，如果该左子树的节点还有左子树，就继续遍历，直至为空
            AftOrder(tnode.RightNode);
            System.out.print(tnode.data);
        }
    }
    public static void main(String[] args) {
        BinaryTree bTree=new BinaryTree();
        System.out.println("请输入二叉树的数据：");
        Scanner in=new Scanner(System.in);
        String TreeStr=in.nextLine();
        Int i=new Int();
        TreeNode s=bTree.CreateTree(TreeStr,i);//创建二叉树,返回的是二叉树的根节点
        System.out.print("中序遍历：");
        bTree.MidOrder(s);
        System.out.println();
        System.out.print("前序遍历：");
        bTree.PreOrder(s);
        System.out.println();
        System.out.print("后序遍历：");
        bTree.AftOrder(s);
    }
}

运行结果：（此处创建二叉树是根据前序遍历的结果来创建的，#表示该节点为空）

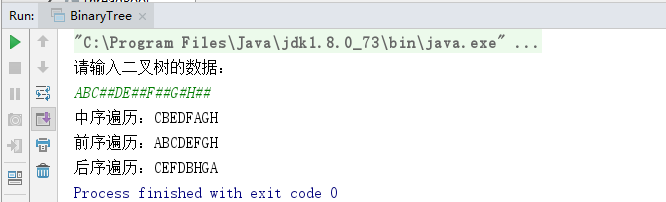
 2.上面是在知道树结构的情况下创建树的，那如果只知道前序和中序，又该如何创建二叉树？(使用中序和后续也是同样的道理)

public class BinaryTree {//用前序和中序来创建二叉树
    public TreeNode CreateTreeByPandM(String Pstr,String Mstr){
        if(Pstr.length()==0||Mstr.length()==0){
            return null;
        }
        char a=Pstr.charAt(0);//子树的根节点
        int index=Mstr.indexOf(a);//根节点在中序遍历中的位置
        TreeNode s=new TreeNode(a);
        s.setLeftNode(CreateTreeByPandM(Pstr.substring(1,index+1),Mstr.substring(0,index)));//substring()方法是前闭后开的
        s.setRightNode(CreateTreeByPandM(Pstr.substring(index+1),Mstr.substring(index+1)));
        return s;
    }//对二叉树进行后序遍历
    public void AftOrder(TreeNode tnode){
        if(tnode!=null){//如果该节点不为null
            AftOrder(tnode.LeftNode);//先遍历该节点左子树，如果该左子树的节点还有左子树，就继续遍历，直至为空
            AftOrder(tnode.RightNode);
            System.out.print(tnode.data);
        }
    }
    public static void main(String[] args) {
        BinaryTree bTree=new BinaryTree()；
        String Pstr="ABCDEFGH";
        String Mstr="CBEDFAGH";
        TreeNode s=bTree.CreateTreeByPandM(Pstr,Mstr);
        System.out.print("后序遍历：");
        bTree.AftOrder(s);
    }
}

 运行结果：

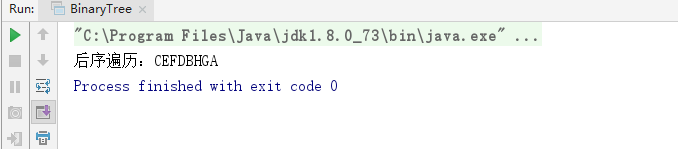
 3.使用非递归的方式进行前中后序的遍历。

public class  BinaryTree {//用中序来创建二叉树
    public TreeNode CreateTreeByPandM(String Pstr,String Mstr){
        if(Pstr.length()==0||Mstr.length()==0){
            return null;
        }
        char a=Pstr.charAt(0);//子树的根节点
        int index=Mstr.indexOf(a);//根节点在中序遍历中的位置
        TreeNode s=new TreeNode(a);
        s.setLeftNode(CreateTreeByPandM(Pstr.substring(1,index+1),Mstr.substring(0,index)));//substring()方法是前闭后开的
        s.setRightNode(CreateTreeByPandM(Pstr.substring(index+1),Mstr.substring(index+1)));
        return s;
    }//非递归的中序遍历
    public void NicePre(TreeNode tnode){
        if (tnode==null)return;
        Stack<TreeNode> stack=new Stack();
        TreeNode pre=tnode;
        while (pre!=null||!stack.empty()){
            while (pre!=null){//该节点不为空，就将其入栈，然后继续遍历其左子树
                stack.push(pre);
                pre=pre.LeftNode;
            }
            TreeNode tn=stack.pop();//左子树为空，就将子树的根节点取出打印
            System.out.print(tn.data);
            pre=tn.RightNode;//接着遍历右子树
        }
    }
    //非递归的前序遍历
    public void NiceMid(TreeNode tnode){
        if (tnode==null)return;
        Stack<TreeNode> stack=new Stack();
        TreeNode pre=tnode;
        while (pre!=null||!stack.empty()){
            while(pre!=null){
                System.out.print(pre.data);//不为空就将其打印，在判断左子树和右子树
                stack.push(pre);
                pre=pre.LeftNode;
            }
            TreeNode tn=stack.pop();
            pre=tn.RightNode;
        }
    }
    //非递归的后序遍历
    public void NiceAft(TreeNode tnode){
        if (tnode==null)return;
        Stack<TreeNode> stack=new Stack();
        TreeNode tag=null;
        TreeNode pre=tnode;
        while (pre!=null||!stack.empty()){
            while(pre!=null){
                stack.push(pre);
                pre=pre.LeftNode;
            }
            TreeNode tn=stack.pop();
            if(tn.RightNode==null||tn.RightNode==tag){//右边为空或右边已被访问过
                System.out.print(tn.data);
                tag=tn;//表示此节点已经被访问过了
                pre=null;
            }else{//右边还未被访问,则先访问右边，同时将根节点又放回栈中
                stack.push(tn);
                pre=tn.RightNode;//设置当前要访问的节点
            }
        }
    }
    public static void main(String[] args) {
        BinaryTree bTree=new BinaryTree()；
        String Pstr="ABCDEFGH";
        String Mstr="CBEDFAGH";
        TreeNode s=bTree.CreateTreeByPandM(Pstr,Mstr)；
        System.out.print("非递归中序遍历：");
        bTree.NicePre(s);
        System.out.println();
        System.out.print("非递归前序遍历：");
        bTree.NiceMid(s);
        System.out.println();
        System.out.print("非递归后序遍历：");
        bTree.NiceAft(s);
        System.out.println();
    }
}

 4.层次遍历。

 public void levelprint(TreeNode tNode){
        ArrayList<TreeNode>  arrayList=new ArrayList<>();
        if(tNode!=null){
            arrayList.add(tNode);
        }
        while (!arrayList.isEmpty()){
            TreeNode tn=arrayList.remove(0);
            System.out.print(tn.data);
            if(tn.LeftNode!=null){
                arrayList.add(tn.LeftNode);
            }
            if(tn.RightNode!=null){
                arrayList.add(tn.RightNode);
            }
        }
    }

 5.锯齿便利，就是下图的遍历方式。

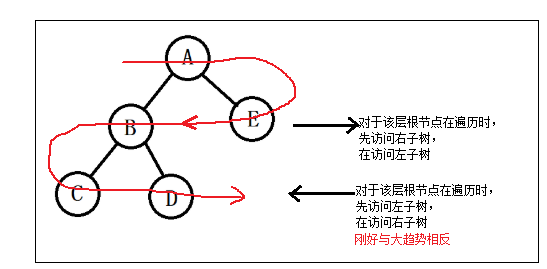
　　此方法的遍历时需借助两个栈，如果将该层的节点在栈A中存放，那么该层节点的子节点就在栈B中存放。

public void juchiprint(TreeNode tNode){
        Stack<TreeNode> stackA=new Stack<>();
        Stack<TreeNode> stackB=new Stack<>();
        if (tNode!=null){//先将根节点存到栈A
            stackA.push(tNode);
        }
        while (!stackA.empty()||!stackB.empty()){
            while (!stackA.empty()){
                TreeNode treeNode=stackA.pop();
                System.out.print(treeNode.data);
　　　　　　      //由于在该层是从右往左遍历，所以该层节点要从左到右存放　　　　
                if (treeNode.LeftNode!=null) stackB.push(treeNode.LeftNode);
                if (treeNode.RightNode!=null) stackB.push(treeNode.RightNode);
            }
            while (!stackB.empty()){
                TreeNode treeNode=stackB.pop();
                System.out.print(treeNode.data);
                //由于在该层是从左往右遍历，所以该层节点要从右到左存放
                if (treeNode.RightNode!=null) stackA.push(treeNode.RightNode);
                if (treeNode.LeftNode!=null) stackA.push(treeNode.LeftNode);
            }
        }
    }

 6.打印指定层。

 //打印二叉树的指定层
    public void LevelIndex(TreeNode root,int index){
        if(index<0) return;
        Stack<TreeNode> stackA=new Stack<>();
        Stack<TreeNode> stackB=new Stack<>();
        ArrayList<String> arrayList=new ArrayList<>();
        StringBuilder sb=new StringBuilder();
        if (root!=null){
            stackA.push(root);
        }
        while (!stackA.empty()||!stackB.empty()){
            while (!stackA.empty()){
                TreeNode treeNode=stackA.pop();
                sb.append(treeNode.data);
                if (treeNode.RightNode!=null) stackB.push(treeNode.RightNode);
                if (treeNode.LeftNode!=null) stackB.push(treeNode.LeftNode);
            }
            arrayList.add(sb.toString());
            sb.delete(0,sb.length());//置空
            while (!stackB.empty()){
                TreeNode treeNode=stackB.pop();
                sb.append(treeNode.data);
                if (treeNode.RightNode!=null) stackA.push(treeNode.RightNode);
                if (treeNode.LeftNode!=null) stackA.push(treeNode.LeftNode);
            }
            arrayList.add(sb.toString());
            sb.delete(0,sb.length());
        }
        System.out.println("第"+index+"层的节点为："+arrayList.remove(2));
    }
    //递归打印二叉树的指定层
    public void LevelIndex2(TreeNode root,int index){
        if(root==null)return;
        if(root!=null&&index==0){//index=0就表示遍历到指定层了
            System.out.println(root.data);
        }else if(root!=null){//当该节点不为空时，且index!=0（也就是还没遍历到指定层时），就继续遍历它的子树
            LevelIndex2(root.LeftNode,index-1); //对于以该节点作为root的子树来说要打印的是第i层，对于它子结点作为root的子树来说要打印的是第i层
            LevelIndex2(root.RightNode,index-1);
        }
    }

 7.打印二叉树的高度（分治思想：根节点的左孩子和右孩子的最大深度值+1）

//打印二叉树的高度（分治思想：根节点的左孩子和右孩子的最大深度值+1）
    public int depth(TreeNode root){
        int num=0;
        if (root==null) return num;
        num=Math.max(depth(root.LeftNode),depth(root.RightNode))+1;
        return num;
    }

8.打印二叉树的节点数（分治思想：左孩子的节点数和右孩子的节点数+1）

 //打印二叉树的节点数（分治思想：左孩子的节点数和右孩子的节点数+1）
    public int NodeNumber(TreeNode root){
        int num=0;
        if (root==null) return num;
        num=NodeNumber(root.RightNode)+NodeNumber(root.LeftNode)+1;
        return num;
    }

 9.查询指定的节点

//查询指定的节点
    public TreeNode Find(TreeNode root,char val){
        if(root==null) return null;//判断空
        if(root.data==val) return root;//先判断根节点是否匹配，匹配就直接返回
        TreeNode LiftNode=Find(root.LeftNode,val);//遍历左子树，查找到返回节点，未查找到返回null
        TreeNode RightNode=Find(root.RightNode,val);//遍历右子树
        //遍历结果有三种，一是在左子树中查找到，二是在右子树中查找到，三是在两棵树中都未查找到
        return LiftNode==null?RightNode:LiftNode;
    }
    public void FindValue(TreeNode root,char val){
        TreeNode ValueNode=Find(root,val);
        if(ValueNode!=null){
            System.out.println(ValueNode.data);
        }else{
            System.out.println("未查找到！");
        }
    }

10.查找孩子的父亲节点

 //查找孩子的父亲节点
 public void getParent(TreeNode root,char child){
        //该节点为空(空树)，或该节点的值等于要查找的孩子节点的值（根节点的值为所要查找的孩子节点的值时，其父亲节点就为null）都返回null
        if(root==null||root.data==child) {
            System.out.println("未查找到！");
        }
        TreeNode ParentNode=get(root,child);
        if(ParentNode!=null){
            System.out.println(ParentNode.data);
        }else{
            System.out.println("未查找到！");
        }
    }
public TreeNode get(TreeNode root,char child){
        if(root.LeftNode==null||root.RightNode==null) return null;
        if(root.LeftNode!=null&&root.LeftNode.data==child){//判断该节点的左右孩子是否匹配，匹配就返回该节点
            return root;
        }
        if(root.RightNode!=null&&root.RightNode.data==child){
            return root;
        }
        TreeNode LiftNode=get(root.LeftNode,child);//在它的左子树中查找
        TreeNode RightNode=get(root.RightNode,child);//在它的右子树中查找
        //遍历结果有三种，一是在左子树中查找到，二是在右子树中查找到，三是在两棵树中都未查找到
        return LiftNode==null?RightNode:LiftNode;
    }

 11.判断是否为满二叉树

 //判断是否为满二叉树
    public boolean judgeFull(TreeNode root){
        ArrayList<TreeNode> arrayList=new ArrayList<>();
        if(root==null) return true;
        arrayList.add(root);
        int n=0;//表示遍历的层数
        int num=1;//表示某层的节点数
        while (!arrayList.isEmpty()){
            if (num==(2^n)){
                int tmp=0;
                for (int i = 0; i <num; i++) {
                    TreeNode node=arrayList.remove(i);
                    if(node.LeftNode!=null){
                        arrayList.add(node.LeftNode);
                        tmp=tmp+1;
                    }
                    if(node.RightNode!=null){
                        arrayList.add(node.RightNode);
                        tmp=tmp+1;
                    }
                }
                num=tmp;
                n=n+1;
            }else {
                return false;
            }
        }
        return true;
    }

12.判断是否为完全二叉树

 思想：将第一层节点存入数组，然后从数组中取数据，不管左右孩子是否存在，每取一次都将它的孩子节点存到数组中，一直反复执行，直到取出一个空节点，如果在这之后从数组中取出的节点都为空就证明该二叉树为完全二叉树，否则不是。

//判断是否为完全二叉树
    public boolean judgeComp(TreeNode root){
        if(root==null) return true;
        ArrayList<TreeNode> arrayList=new ArrayList<>();
        arrayList.add(root);
        while (!arrayList.isEmpty()){
            TreeNode node=arrayList.remove(0);
            if(node!=null){
                arrayList.add(node.LeftNode);
                arrayList.add(node.RightNode);
            }else {
                while (!arrayList.isEmpty()){
                    TreeNode node2=arrayList.remove(0);
                    if(node2!=null){
                        return false;
                    }
                }
            }
        }
        return true;
    }

 13.用顺序存储的二叉树数组来创建链式的二叉树，前中后序的遍历过程。

class TNode{
    TNode RightNode;
    TNode LiftNode;
    Object data;
    public TNode(Object data){
        this.data=data;
    }
    public void setRightNode(TNode rightNode) {
        RightNode = rightNode;
    }
    public void setLiftNode(TNode liftNode) {
        LiftNode = liftNode;
    }
}
public class Array_BinaryTree {
    private static TNode Create(int[] arr,int i) {
        if(arr.length>arr.length) return null;
        TNode root=new TNode(arr[i]);//创建头节点
        if (2*i+1<arr.length&&arr[2*i+1]!=-1){
            root.setLiftNode(Create(arr,2*i+1));//递归创建左子树
        }
        if (2*i+2<arr.length&&arr[2*i+2]!=-1){
            root.setRightNode(Create(arr,2*i+2));//递归创建右子树
        }
        return root;
    }
    private static Object CreateTree(int[] arr,int index) {
        if (arr.length == 0 || index < 0) return null;
        TNode node=Create(arr,index);
        if(node!=null) return node.data;
        return null;
    }
    private static void preArray(int[] arr,int index) {
        if(index<0||index>arr.length-1) return;
        if (arr[index]!=-1){
            System.out.print(arr[index]+",");
            preArray(arr,2*index+1);
            preArray(arr,2*index+2);
        }
    }
    private static void midArray(int[] arr,int index) {
        if(index<0||index>arr.length-1) return;
        if (arr[index]!=-1){
            midArray(arr,2*index+1);
            System.out.print(arr[index]+",");
            midArray(arr,2*index+2);
        }
    }
    public static void aftArray(int[] arr,int index){
        if(index<0||index>arr.length-1) return;
        if (arr[index]!=-1){
            aftArray(arr,2*index+1);
            aftArray(arr,2*index+2);
            System.out.print(arr[index]+",");
        }
    }
    public static void main(String[] args) {
        int[] arr=new int[]{31,23,12,66,-1,5,17,70,62,-1,-1,-1,88,-1,55};
        System.out.println(CreateTree(arr,0));
        preArray(arr,0);
        System.out.println();
        midArray(arr,0);
        System.out.println();
        aftArray(arr,0);
    }
}

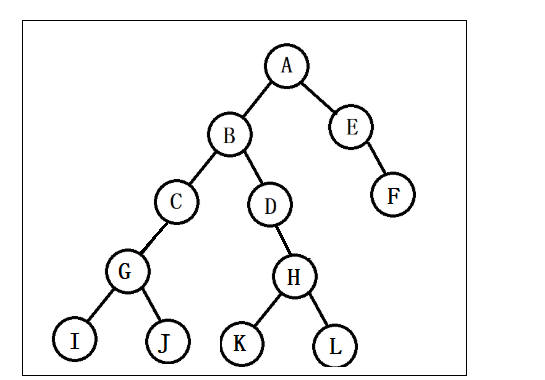
假设我们现在有这样一组数[35 27 48 12 29 38 55]，顺序的插入到一个数的结构中， 

                   

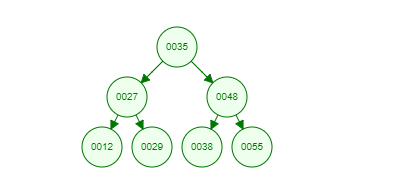
        这就是一棵二叉树啦！我们能看到，经通过一系列的插入操作之后，原本无序的一组数已经变成一个有序的结构了，并且这个树满足了上面提到的两个二叉树的特性！

  但是如果同样是上面那一组数，我们自己升序排列后再插入，也就是说按照[12 27 29 35 38 48 55]的顺序插入，会怎么样呢？

                        

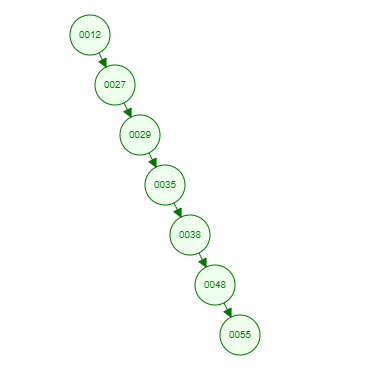
       由于是升序插入，新插入的数据总是比已存在的结点数据都要大，所以每次都会往结点的右边插入，最终导致这棵树严重偏科！！！上图就是最坏的情况，也就是一棵树退化为一个线性链表了，这样查找效率自然就低了，完全没有发挥树的优势了呢！
为了较大发挥二叉树的查找效率，让二叉树不再偏科，保持各科平衡，所以有了平衡二叉树！

平衡二叉树

 平衡二叉树是一种特殊的二叉树，所以他也满足前面说到的二叉树的两个特性，同时还有一个特性：

它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

  大家也看到了前面[35 27 48 12 29 38 55]插入完成后的图，其实就已经是一颗平衡二叉树啦。

  那如果按照[12 27 29 35 38 48 55]的顺序插入一颗平衡二叉树，会怎么样呢？我们看看插入以及平衡的过程：

 

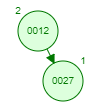
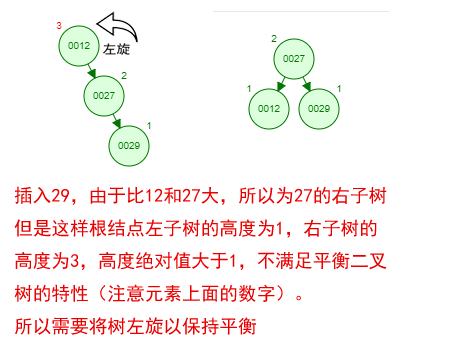
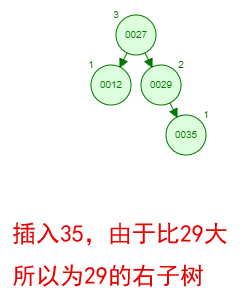
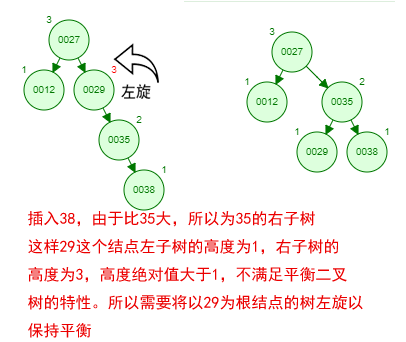
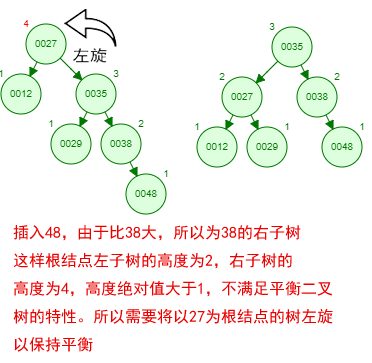
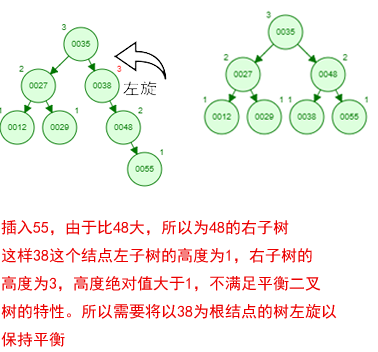
 这棵树始终满足平衡二叉树的几个特性而保持平衡！这样我们的树也不会退化为线性链表了！我们需要查找一个数的时候就能沿着树根一直往下找，这样的查找效率和二分法查找是一样的呢！

  一颗平衡二叉树能容纳多少的结点呢？这跟树的高度是有关系的，假设树的高度为h，那每一层最多容纳的结点数量为2^(n-1)，整棵树最多容纳节点数为2^0+2^1+2^2+...+2^(h-1)。这样计算，100w数据树的高度大概在20左右，那也就是说从有着100w条数据的平衡二叉树中找一个数据，最坏的情况下需要20次查找。如果是内存操作，效率也是很高的！但是我们数据库中的数据基本都是放在磁盘中的，每读取一个二叉树的结点就是一次磁盘IO，这样我们找一条数据如果要经过20次磁盘的IO？那性能就成了一个很大的问题了！那我们是不是可以把这棵树压缩一下，让每一层能够容纳更多的节点呢？虽然我矮，但是我胖啊... 因此就引入了B-树和B+树。。。