-2.风险人群筛查

样例输入1
5 2 6 20 40 100 80
100 80 100 80 100 80 100 80 100 80 100 80
60 50 60 46 60 42 60 38 60 34 60 30
10 60 14 62 18 66 22 74 26 86 30 100
90 31 94 35 98 39 102 43 106 47 110 51
0 20 4 20 8 20 12 20 16 20 20 20
样例输出1
3
2
样例输入2
1 3 8 0 0 10 10
-1 -1 0 0 0 0 -1 -1 0 0 -1 -1 0 0 0 0
样例输出2
1
0
样例2说明
该位置记录经过了高危区域,但最多只有连续两个时刻位于其中,不满足逗留条件。
#include<iostream>
#include<vector>
using namespace std;
int n;
int k;
int t;
int xl;
int xr;
int yd;
int yu;
int ans1=0;//经过
int ans2=0;//逗留
class Point{
public:
int x;
int y;
};
//判断点是否在区域内
int judge(Point p){
if(xl<=p.x&&p.x<=xr&&yd<=p.y&&p.y<=yu) return 1;
return 0;
}
int main(){
cin>>n>>k>>t>>xl>>yd>>xr>>yu;
vector<Point> v[n];
for(int i=0;i<n;i++){
for(int j=0;j<t;j++){
int x,y;
cin>>x>>y;
Point p = {x,y};
v[i].push_back(p);
}
}
for(int i=0;i<n;i++){
int flag= 0;
//前一个是否在区域内
int maxn = 0;
int tmp = 0;
//记录最大连续个数
for(int j=0;j<t;j++){
if(judge(v[i][j])) {
if(flag) tmp++;
else{
tmp++;
flag=1;
}
maxn=max(maxn,tmp);
}else{
flag=0;
tmp=0;
}
}
if(maxn>=k) {
ans1++;
ans2++;
}else if(maxn>=1) ans1++;
}
cout<<ans1<<endl;
cout<<ans2;
return 0;
}




样例输入1
1
3 5
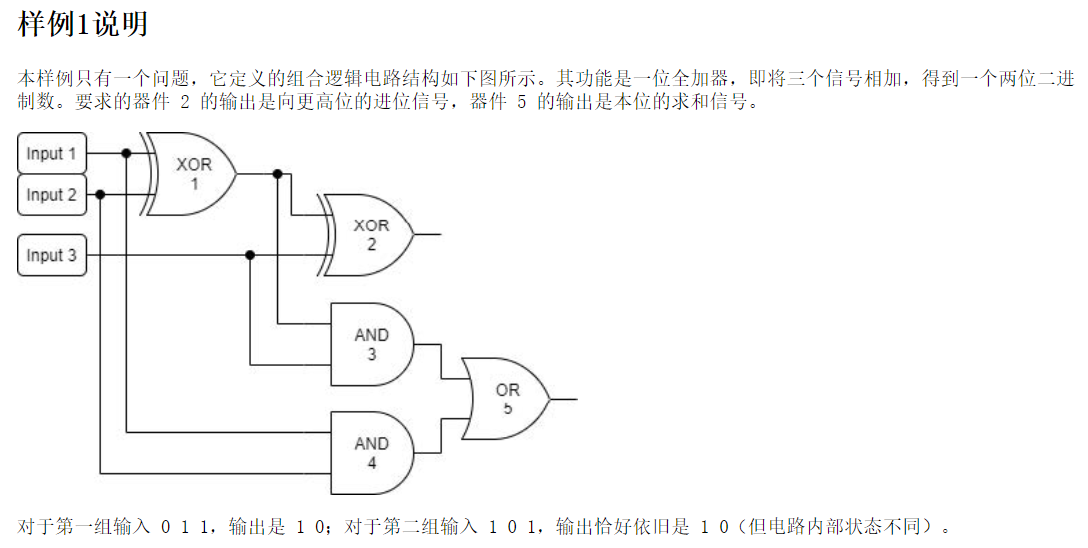
XOR 2 I1 I2
XOR 2 O1 I3
AND 2 O1 I3
AND 2 I1 I2
OR 2 O3 O4
4
0 1 1
1 0 1
1 1 1
0 0 0
2 5 2
2 5 2
2 5 2
2 5 2
样例输出1
1 0
1 0
1 1
0 0
样例输入2
1
2 6
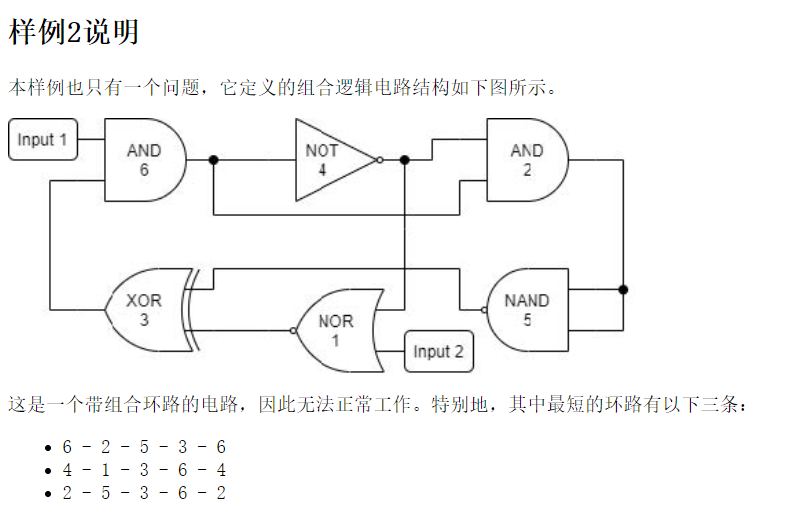
NOR 2 O4 I2
AND 2 O4 O6
XOR 2 O5 O1
NOT 1 O6
NAND 2 O2 O2
AND 2 I1 O3
2
0 0
1 0
3 2 3 4
6 1 2 3 4 5 6
样例输出2
LOOP

/*
1
3 5
XOR 2 I1 I2
XOR 2 O1 I3
AND 2 O1 I3
AND 2 I1 I2
OR 2 O3 O4
4
0 1 1
1 0 1
1 1 1
0 0 0
2 5 2
2 5 2
2 5 2
2 5 2
*/
//记忆化搜索+拓扑排序判环
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5;
struct Node{
int opt;
vector<int>In;
//cin的输入
vector<int>Out;
//把其他器件的输出作为输入
}Dev[505];
int Input[N][505];//输入的0 1操作
int Ind[505];//每个器件的入度
int ans[505];//记录每个器件的结果
vector<int>e[505];//邻接表
int getNum(int pos,char *str){
int num=0;
int len=strlen(str);
while(pos<len){
num=num*10+str[pos]-'0';
++pos;
}
return num;
}
int Operation(vector<int>q,int opt){
if(opt==0) return !q[0];
else{
int cnt=q.size();
int r=q[0];
if(opt==1){
for(int i=1;i<cnt;++i) r&=q[i];
return r;
}
else if(opt==2){
for(int i=1;i<cnt;++i) r|=q[i];
return r;
}
else if(opt==3){
for(int i=1;i<cnt;++i) r^=q[i];
return r;
}
else if(opt==4){
for(int i=1;i<cnt;++i) r&=q[i];
return !r;
}
for(int i=1;i<cnt;++i) r|=q[i];
return !r;
}
}
int dfs(int s,int u){
if(ans[u]!=-1) return ans[u];
int cnt=Dev[u].In.size();
vector<int>t;
for(int i=0;i<cnt;++i){
t.push_back(Input[s][Dev[u].In[i]]);
}
cnt=Dev[u].Out.size();
for(int i=0;i<cnt;++i){
t.push_back(dfs(s,Dev[u].Out[i]));
}
return ans[u]=Operation(t,Dev[u].opt);
}
bool topolog(int n){
queue<int>Q;
for(int i=1;i<=n;++i){
if(!Ind[i]) Q.push(i);
}
int cnt=0;
while(!Q.empty()){
int u=Q.front();
Q.pop();
++cnt;
int cnt=e[u].size();
for(int i=0;i<cnt;++i){
int v=e[u][i];
if(!(--Ind[v])) Q.push(v);
}
}
return cnt==n;
}
int main(){
map<string,int>Mp;
Mp["NOT"]=0;Mp["AND"]=1;Mp["OR"]=2;Mp["XOR"]=3;Mp["NAND"]=4;Mp["NOR"]=5;
char str[10];
int Q;scanf("%d",&Q);
while(Q--){
int m,n;scanf("%d%d",&m,&n); //输入个数和器件数量
//清空上一次的内容
for(int i=1;i<=n;++i){
e[i].clear();
Ind[i]=0;
Dev[i].In.clear();
Dev[i].Out.clear();
}
for(int i=1;i<=n;++i){ //每个器件
scanf("%s",str);
Dev[i].opt=Mp[str];
int k;scanf("%d",&k);
//k为该器件输入个数
for(int j=0;j<k;++j){
scanf("%s",str);
int num=getNum(1,str);
//将O或者I后面的数字取出
//构造有向图
if(str[0]=='I') Dev[i].In.push_back(num);
else{
e[num].push_back(i);
Ind[i]++;
Dev[i].Out.push_back(num);
}
}
}
int S;scanf("%d",&S);
//S为重复次数,即输入的组数
for(int i=0;i<S;++i){
for(int j=1;j<=m;++j) scanf("%d",&Input[i][j]);
}
bool fg=topolog(n);
if(!fg) puts("LOOP");
for(int i=0;i<S;++i){
int s,num;scanf("%d",&s);
//s输出的器件个数
memset(ans,-1,sizeof(ans));
for(int j=0;j<s;++j){
scanf("%d",&num);
if(fg) printf("%d%c",dfs(i,num),j==s-1?'\n':' ');
}
}
}
return 0;
}