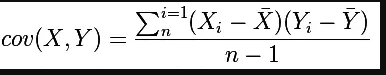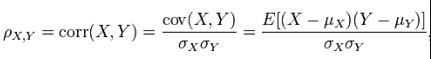一、为什么做特征选择
- 提升效果,让分类更准确和泛化效果更好。奥卡姆剃刀原理告诉我们“若无必要,勿增实体”。特征的增多会大大增加分类算法求解的搜索空间,大多数训练算法所需样本数量随着不相关特征数量的增加而显著增加。除了识别和去除出不相关的特征和冗余的特征外,一些特征添加后虽然能让模型更好的拟合训练数据,但因为复杂度的增加导致模型有更高的variance误差,过拟合的后果是在测试数据集上效果反而不好。
- 改善性能,节省存储和计算开销。在数据的处理和模型的训练过程中一般有很多参数(数据时间窗口长度,特征离散化方法,正则化系数等等)可以调节,让从数据产生到得到最终模型的时间更短,速度的提升意味着可以尝试更多的参数,更优的参数也会带来效果的改善。快速迭代是持续提升效果所需的关键能力之一。
- 更好的模型可解释性。在一些应用场景下,比起一个表现95分的黑盒模型我们可能更喜欢一个表现90分的白盒模型。可解释不仅让我们对模型效果的稳定性有更多的把握,一个可读懂的模型所提供的知识也能为我们的业务运营等工作提供指引和决策支持。以决策树为例,只有几个分支的一棵树肯定比一颗有几百个分支的树让人更容易分析和理解。
二、特征选择的常用方法
2. 1 Filter
Filter方法是选定一个指标来评估特征,根据指标值来对特征排序,去掉达不到足够分数的特征。这类方法只考虑特征X和目标Y之间的关联,相对另两类特征选择方法Wrapper和Embedded计算开销最少,特征选择过程与后续学习器无关。指标的选择对Filter方法至关重要,下面我们就看几种被大家通常使用的指标。
统计的视角:
- 相关系数(Correlation)。统计课本里都讲过的皮尔森相关系数是最常用的方法。需要注意的是当样本数很少或者特征的取值范围更广时,更容易得出绝对值更大的皮尔森系数,所以样本量不同或者取值范围不同的特征的之间相关系数不一定可以做比较。另外皮尔森相关系数只能衡量线性相关性,随机变量X和Y不相关并不意味二者独立。当相关系数为0时我们知道的是线性分类器不能单利用这个特征的目前的形态做到将不同的类分开,但通过特征本身的变换、和其它特征组合使用或者与其它特征结合出新的特征却可能让它焕发出生机发挥出价值。
- 假设检验(Hypothesis Testing)。将特征X和目标Y之间独立作为H0假设,选择检验方法计算统计量,然后根据统计量确定P值做出统计推断。
信息论的视角:
- 互信息
- 信息增益
协方差:
皮尔逊相关系数:协方差除以两个变量的标准差
虽然协方差能反映两个随机变量的相关程度(协方差大于0的时候表示两者正相关,小于0的时候表示两者负相关),但是协方差值的大小并不能很好地度量两个随机变量的关联程度,例如,现在二维空间中分布着一些数据,我们想知道数据点坐标X轴和Y轴的相关程度,如果X与Y的相关程度较小但是数据分布的比较离散,这样会导致求出的协方差值较大,用这个值来度量相关程度是不合理的pearson相关系数是一个介于-1和1之间的值,当两个变量的线性关系增强时,相关系数趋于1或-1;当一个变量增大,另一个变量也增大时,表明它们之间是正相关的,相关系数大于0;如果一个变量增大,另一个变量却减小,表明它们之间是负相关的,相关系数小于0;如果相关系数等于0,表明它们之间不存在线性相关关系。皮尔逊相关系数是对协方差的修正。
2.2 Wrapper
Wrapper方法和Filter不同,它不单看特征X和目标Y直接的关联性,而是从添加这个特征后模型最终的表现来评估特征的好坏,即直接把最终将要使用的学习器的性能作为特征子集的评价标准。Wrapper方法需要选定一种评估模型效果的指标,如Area Under the Curve (AUC)、Mean Absolute Error (MAE)、Mean Squared Error(MSE)。假设我们有N个特征,除去空集外这N个特征可以组成2N−1个集合,最暴力的方法是分别用2N−1个特征集合训练得到模型做评估,最后选择模型效果最好的集合。显而易见当N很大时穷举法计算开销惊人。所以前向特征选择(Forward Feature Selection)和后向特征选择(Backward Feature Selection)这样的贪心策略更为大家平常所用。前向特征选择从空集开始,每次在现有特征集合的基础上添加一个让模型效果最好的特征。相反,后向特征选择一开始包括所有的候选特征,每次去掉一个让模型指标提升最多的特征。
离线评估结果是重要的参考指标,但在实际应用中,往往最终还是通过线上A/B Test实验来判断一个特征的效果。在实际应用中离线评估不错的特征在线上表现不一定就好,线上线下评估的一致性和影响因素是另一个可以值得研究的问题。
2.3 Embedded
Filter方法和Wrapper方法都是和分类算法本身的实现无关,可以与各种算法结合使用。而Embedded特征选择方法与算法本身紧密结合,在模型训练过程中完成特征的选择。例如:决策树算法每次都优先选择分类能力最强的特征;逻辑回归算法的优化目标函数在log likelihood的基础上加上对权重的L1或者L2等罚项后也会让信号弱的特征权重很小甚至为0。
一些优化算法天然就适合在每步判断一个维度特征的好坏,所以可以在学习器在设计时就同时融合了特征选择功能,在训练过程中自动尝试构造特征和选择特征。
小结
Filter、Wrapper、Embedded三种方法各有不同,但没有孰好孰坏之分,在我们的实际工作中会结合使用。Filter作为简单快速的特征检验方法,可以指导特征的预处理和特征的初选。Embedded特征选择是我们学习器本身所具备的能力。通过Wrapper来离线和在线评估是否增加一个特征。数据挖掘竞赛中一般预处理时候使用filter,然后可以利用embedded输出特征的重要性,主要还是根据业务构造特征,然后使用wrapper来一个个评估特征。