codeforces 878C

http://codeforces.com/contest/878/problem/C

题意：一共有 k 种比赛项目，有 n 次询问，第 i 次询问有 i 支队伍参加比赛（在第 i-1 次询问基础上增加一支），第 i 次询问会举行 i 场比赛，从 k 种项目种任选一场，i 支队伍中任选二支，输的一方退场，赢的留下。倘若队伍 a 和 队伍 b 比赛，比赛项目为 j ，若队伍 a 在项目 j 的力量大于队伍 b 在项目 j 的比重，则 a 赢，反之 b 赢。问每次询问最后能获得冠军的队伍有几支。

题解：若队伍 a 在某种比赛中能打败 队伍 b，则有一条 a 指向 b 的路径， 将联通块（可以互相到达的点）缩为一点，最后入度为 0 的点为可以获胜的点，求这个点里面包含几只队伍。

本来想的是 Targin 缩点，再并查集，看看能不能过去。看了某大神的代码，学习了一波 http://www.cnblogs.com/qscqesze/p/7762484.html ozr！

 一开始很想不明白 set::lower_bound 和 set::upper_bound 为什么会找到不同的点。

看了一下源码

lower_bound的实现，它的比较函数是 树的结点 与 传进去的结点 进行比较，调用了 < 的比较符。

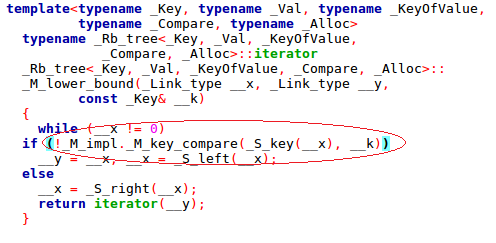
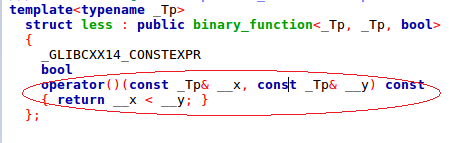
upper_bound的实现，它的比较函数是 传进去的结点 与 树的结点 进行比较，同样调用了 < 的比较符。

 

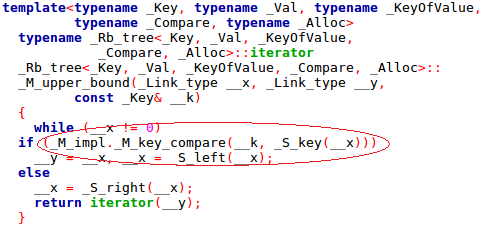
AC代码

#include <iostream>
#include <set>
#include <cstdio>
using namespace std;
int n, k;
struct node
{
    int mi[12], mx[12], s;
    bool operator < (const node a)const
    {
        for(int i = 1; i <= k; ++i)
        {
            if(mx[i] > a.mi[i]) return false;
        }
        return true;
    }
};
set<node> se;
int main()
{
    cin >> n >> k;
    for(int i = 1; i <= n; ++i)
    {
        node nod; nod.s = 1;
        for(int j = 1; j <= k; ++j)
        {
            int c;  cin >> c;
            nod.mi[j] = nod.mx[j] = c;
        }
        set<node>::iterator x = se.lower_bound(nod);
        set<node>::iterator y = se.upper_bound(nod);
        while(x != y)
        {
            for(int j = 1; j <= k; ++j)
            {
                nod.mi[j] = min(nod.mi[j], x->mi[j]);
                nod.mx[j] = max(nod.mx[j], x->mx[j]);
            }
            nod.s += x->s;
            se.erase(x++);
        }
        se.insert(nod);
        cout << se.rbegin()->s << endl;
    }
}