斐波那契数列改进

#include<iostream>
using namespace std;
   
   int Fib(int n)
   {
       static int a[50]={0};       //  此处数组必须声明为static，否则会运行极慢！因为如果是普通数组，递归调用每调用一次就定义一次。而static变量只会定义一次。
       if(n<=1)
           return 1;
       if(!a[n-2])                 //  为防止重复计算，使用数组存储已经计算出的值。
          a[n-2] = Fib(n-2);
       if(!a[n-1])
          a[n-1] = Fib(n-1);
      return a[n-2]+a[n-1];
   }
  
  int main()
  {
      int n;
      cout<<"Please enter a number :";
      cin>>n;
      cout<<Fib(n)<<endl;
  
  }         

还有一种是通过尾递归优化：

解决递归调用栈溢出的方法是通过尾递归优化，事实上尾递归和循环的效果是一样的，所以，把循环看成是一种特殊的尾递归函数也是可以的。

尾递归是指，在函数返回的时候，调用自身本身，并且，return语句不能包含表达式。这样，编译器或者解释器就可以把尾递归做优化，使递归本身无论调用多少次，都只占用一个栈帧，不会出现栈溢出的情况。

递归的第一次调用时会开辟一份空间，此后的递归调用不会再开辟空间，而是在刚才开辟的空间上做一些修改，实现此次递归，例如求Fib（10），编译器会给Fib（10）的调用开辟栈帧，调用Fib（9）的时候不会再重新开辟栈帧，而是在刚开辟的栈帧上做一些修改，因为递归的每一次调用都是一样的流程，只是会有一些数据不同，所以不会再开辟空间。

上面的fact(n)函数由于return n * fact(n - 1)引入了乘法表达式，所以就不是尾递归了。

int Fib(int first,int second ,int N)
{
    if (N < 3)
        return 1;
    if (N == 3)
        return first + second;
    return Fib(second, first + second, N - 1);
}

再有就是通过循环来实现，效率也是最高的。

int Fib(int N)
{
        int first = 1;
        int second = 1;
        int ret = 0;
        for(int i =3;i<=N;++i){
                ret = first + second;
                first = second;
                second = ret;
        }
        return second;
}
    

效率最低的：

int Fib(int N)
{
        if(N<3)
            return 1;
        return Fib(N-1)+Fib(N-2);
}

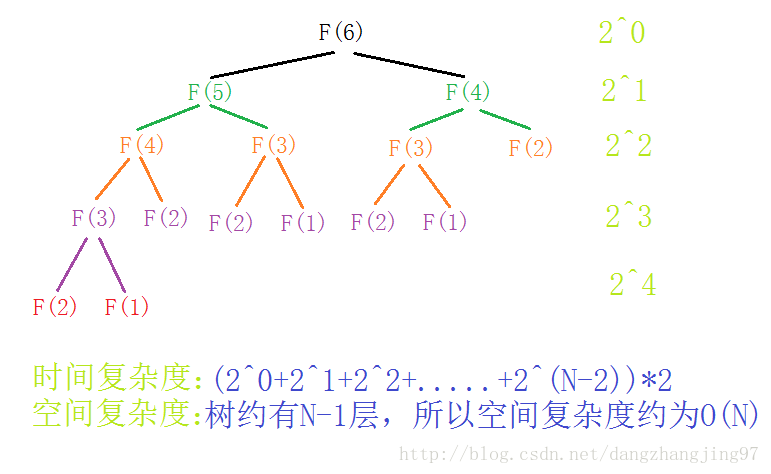
可以看出 F(3)就被计算了3次。

参考：https://blog.csdn.net/MallowFlower/article/details/78858553