线性回归中提到最小二乘损失函数及其相关知识。对于这一部分知识不清楚的同学能够參考上一篇文章《线性回归、梯度下降》。
本篇文章主要解说使用最小二乘法法构建损失函数和最小化损失函数的方法。
最小二乘法构建损失函数
最小二乘法也一种优化方法，用于求得目标函数的最优值。简单的说就是：让我们的预測值与真实值总的拟合误差（即总残差）达到最小。
在线性回归中使用最小二乘法构建了损失函数：
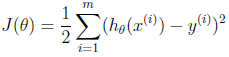
上一篇文章《线性回归、梯度下降》中提到求解使损失函数J(θ)取最小的θ值有两种方法：梯度下降（gradient descent）和正则方程（The normal equations）。以下主要讲一下正则方程。梯度下降方法最小化损失函数參考文章《线性回归、梯度下降》
正则方程
将训练特征表示为X矩阵，结果表示成y向量，仍然是线性回归模型。损失函数不变。那么θ能够直接由以下公式得出：
推导过程涉及线性代数方面的知识，这里不再具体展开线性代数知识。
设m为训练样本数；x为样本中的自变量，即二手房价格预測中的房屋面积和我是数目。x为n维向量；向量y为训练数据中的房屋价格。y为m维向量。那么训练数据能够用矩阵表示为：
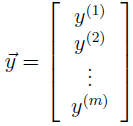
由于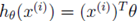
，所以
就能够表示为：
损失函数就转化为：
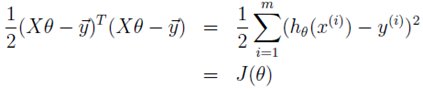
线性代数中有两个公式：
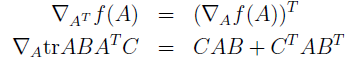
当中符号
表示一个m*n的矩阵。这个矩阵的第(i,j)个元素为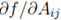
。
上面两个公式合起来能够表示为：
根据这这个公式对损失函数J(θ)推导：
为了最小化J(θ)。又由于J(θ)由最小二乘法得到，J(θ)的取值大于等于0。即最小值为0。
所以，我们使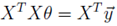
，从而得到θ取值：
