在上一篇博客判断有向图是否有圈中从递归的角度简单感性的介绍了如何修改深度优先搜索来判断一个有向图是否有圈。事实上, 它的实质是利用了深度优先生成树(depth-first spanning tree)的性质。那么什么是深度优先生成树?顾名思义,这颗树由深度优先搜索而生成的,由于无向图与有向图的深度优先生成树有差别,下面将分别介绍。
一. 无向图的深度优先生成树
无向图的深度优先生成树的生成步骤:
- 深度优先搜索第一个被访问的顶点为该树的根结点。
- 对于顶点v,其相邻的边w如果未被访问,则边(v, w)为该树的树边,用实线表示;若w已经被访问,则边(v, w)为该树的回退边(back edge),用虚线表示(代表这条边实际上不是树的一部分)。
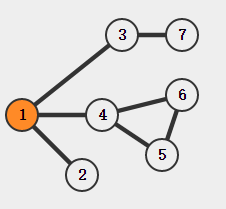
下面是一个无向图和它对应的深度优先生成树:
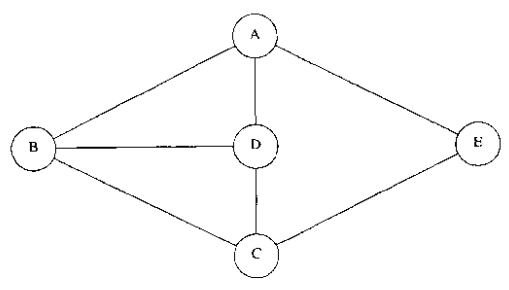
不难发现,该树的先序遍历过程就是DFS过程,利用该树我们可以更好的理解DFS。而对无向图而言,深度优先生成树一个重要的应用是解决
双连通性问题(该问题在通讯网络,运输网络等有重要应用)。当然,我们首先需要了解双连通性问题的相关概念。
- 如果一个连通的无向图中的任一顶点被删除后,剩下的图仍然连通,那么这样的无向连通图就称作是双连通的(biconnected)。(上图的无向图是双连通的)
- 如果一个图不是双连通的,也就是说存在一些顶点,将其删除后图将不在连通,我们把那些顶点称为割点或者关节点(articulation point)。
下图是一个不是双连通的图,其中顶点C和D为割点。
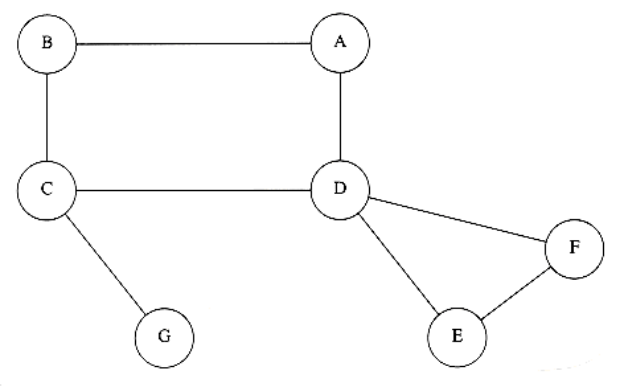
利用深度优先生成树求连通图中的所有割点算法如下:
- 通过先序遍历深度优先生成树获得每个顶点的先序编号(也是深度优先编号),不妨把顶点v的先序编号记为num(v);
- 计算深度优先生成树上的每一个顶点的最小编号,所谓最小编号是取顶点v和w的先序编号的较小者,其中的w是从v点沿着零条或多条树边到v的后代x(可能是v本身),以及可能沿着任意一条回退边(x,w)所能达到w的所有顶点,记为low(v)。由low(v)的定义可知low(v)是:(1). num(v);(2). 所有回退边(v, w)中的最小num(w);(3). 所有树边(v, w)中的最小low(w)三者中的最小值。由(3)可知我们必须先求出v的所有孩子的最小编号,故需要用后序遍历计算low(v)。
- 求出所有割点:
- 第一类割点:根节点是割点当且仅当他有两个或两个以上的孩子。因为如果根节点有多个孩子时,删除根使得其他的节点分布在不同的子树上,而每一棵子树就对应一个连通图,所以整个图就不连通了;而但根只有一个孩子时,删除它还是只有一棵子树。
- 第二类割点:对于除根节点以外的节点v,它是割点当且仅当它有某个孩子使得low(w) >= num(v),即以v为根节点的子树中的所有节点均没有指向v的祖先的背向边,这样若删除v,其子树就和其他部分分开了。(注意:节点v一定不是叶节点因为删除叶节点还是一棵树,而根节点之所有单独拿出来是因为任何情况下若v为根节点,一定满足low(w) >= num(v),因为num(v)是最小先序编号)。
下面是分别从A与C开始遍历上图生成的树:
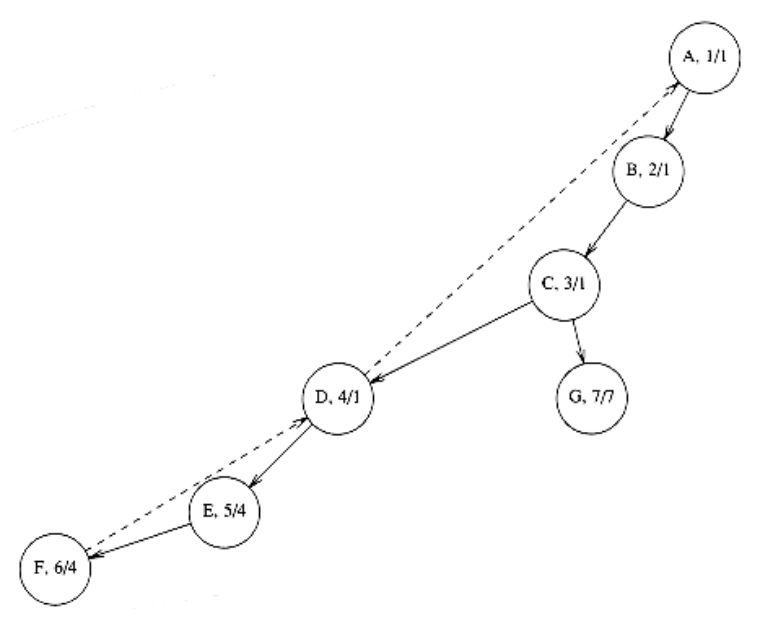
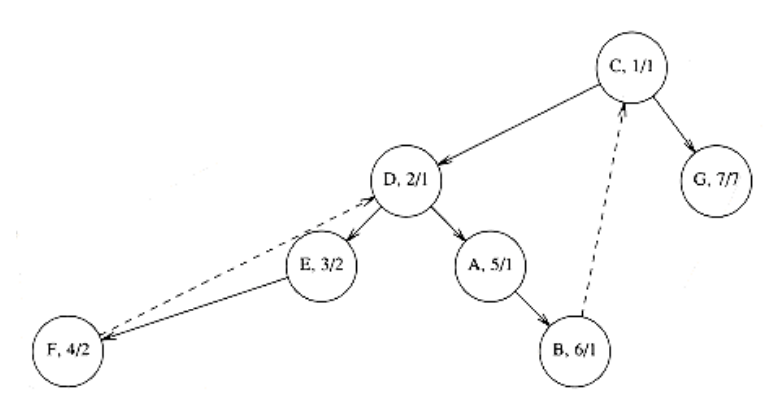
c++实现代码如下:
/*
数据结构:邻接表存储图
程序说明:为简单起见,设节点的类型为整型,设visited[],num[].low[],parent[]为全局变量,
为求得先序编号num[],设置全局变量counter并初始化为1。为便于单独处理根节点设置root变量。
*/
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int MAX_N = 100;
vector<int> graph[MAX_N];
vector<int> artPoint;
int num[MAX_N], low[MAX_N], parent[MAX_N];
int counter = 1;
int root;
bool visited[MAX_N];
void Init(); //初始化图
void FindArt(int v); //找到第二类割点
void PrintArtPoint(); //打印所有割点(第一类割点在此单独处理)
int main()
{
Init();
FindArt(root);
PrintArtPoint();
return 0;
}
void PrintArtPoint()
{
int rootChild = 0; //根节点的孩子个数
for (int i = 0; i < graph[root].size(); i++) //计算根节点的孩子个数
{
if (parent[graph[root][i]] == root)
rootChild++;
}
if (rootChild > 1) //根节点孩子个数大于1则为割点
artPoint.push_back(root);
for (int i = 0; i < artPoint.size(); i++)
printf("%d
", artPoint[i]);
}
void Init()
{
int a, b;
root = 1;
while (scanf("%d%d", &a, &b) != EOF)
{
graph[a].push_back(b);
graph[b].push_back(a);
visited[a] = false;
visited[b] = false;
}
}
void FindArt(int v)
{
visited[v] = true;
low[v] = num[v] = counter++; //情况(1)
for (int i = 0; i < graph[v].size(); i++)
{
int w = graph[v][i];
if (!visited[w]) //树边
{
parent[w] = v;
FindArt(w);
if (low[w] >= num[v] && v != root)
artPoint.push_back(v);
low[v] = min(low[v], low[w]); //情况(3)
}
else if (parent[v] != w) //回退边
{
low[v] = min(low[v], num[w]); //情况(2)
}
}
}
测试运行结果如下:
二. 有向图的深度优先生成树
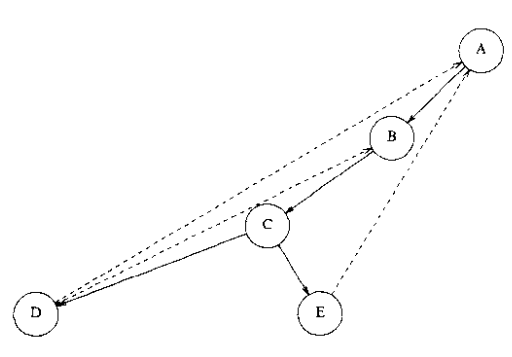
我们知道有向图同样可以和无向图一样进行深度优先搜索。但是,由于有向图的特点:边的方向性导致即使两个顶点有边相连也不一定是可达的,有向图的深度优先生成树的边有了更多的情况,包括树边(tree edges), 回退边(back edges),向前边(forward edges), 横边(cross edges)。其中后三者是树实际不存在的边,通向的是已经被访问过的点。下面用一张图来直观感受一下这几种情况:
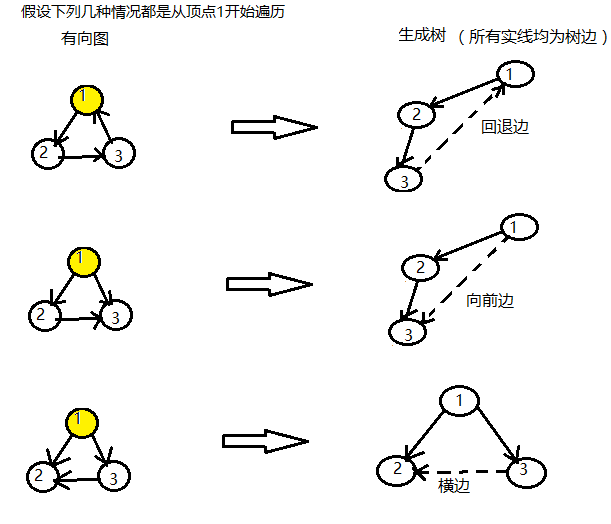
事实上,有以下结论(其中num[]保存的是树节点的先序序列即DFS序列):
1、若num[v] < num[w],即v在w之后被访问,则(v,w)是树边或向前边;
此时,若visited[v]= true, visited[w] = false,(v,w)为 树边;
若visited[v]= true, visited[w] = true,(v,w) 为 向前边;比如上图的第2种情况,访问到节点3时,节点1已经被访问,且num[1]<num[3],故边(1, 3)是向前边。
2、若num[v] > num[w],即v在w之后被访问,故visited[v] = true则visited[w] = true,则(v,w)是回退边或横边;
当产生树边(i,j) 时,同时记下j的父节点:parent[j] = i, 于是对图中任一条边(v,w),由结点v沿着树边向上(parent中)查找w(可能直到根);
若找到w,则(v,w)是回退边,否则是横边。比如上图第一种情况parent[3] = 1,故边(3, 1)为回退边,而第3种情况节点3无父节点,故为横边。
到此我们就知道了如下法则:一个有向图是无圈图当且仅当它没有回退边。
查找强连通分量(SCC: Strong Connected Components)
有向图的深度优先生成树除了可以用于判断有向图是否有边,还可以用来查找强连通分量。首先给出相关概念:
强连通图:一个有向图中任意两个顶点是可以互达的。
强连通分量:对于一个非强连通图,我们可得到顶点的一些子集,使得它们到自身是强连通的。
查找强连通分量的算法:
1. Kosaraju-Sharir算法
- 首先对输入的图G进行一次DFS:后序遍历深度优先生成森林,将图G的顶点标号。然后将图G所有边反向,得到Gr。
- 每次在图Gr中还未访问的顶点中从编号最大的顶点开始对Gr进行DFS,每进行一次DFS得到的深度优先生成树中的所有顶点就是一个强连通分量;如此直到所有点被访问。
理解该算法:如果两个顶点v和w都在一个强连通分支中,则原图G中就存在v到w和w到v的路径,所以Gr也存在。 而两个顶点互达与这两个顶点在Gr中 的同一棵深度优先生成树等价。所以步骤2每次DFS都能得到一个强连通分量。
代码如下:
/*
数据结构;邻接表
程序说明:1. 每对Gr进行一次DFS,生成一个强连通分量,topSort++,
所以topSort相同的顶点即在同一个强连通分量中。
2. 为便于得到最大编号对应的顶点,设置node[],其下标为后序编号,值为对应顶点
*/
#include <cstdio>
#include <vector>
#include <cstring>
#include <cstdlib>
using namespace std;
const int MAX_N = 100;
vector<int> G[MAX_N]; //原图
vector<int> Gr[MAX_N]; //反转后的图
vector<int> topSort[MAX_N]; //下标为所属强分支的拓扑序
int counter = 0; //用于编号
int node[MAX_N]; //后序遍历标号,下标为编号
bool visited[MAX_N];
int vNum; //图的顶点数
void DFS(int v);
void RDFS(int v, int k); //参数k为v所在的强连通分量的拓扑序
int SCC(); //返回强连通分量的个数
void Init(); //初始化图G和Gr
int main()
{
Init();
int sccNum = SCC();
printf("%d
", sccNum);
for (int i = 0; i < sccNum; i++)
{
int j;
printf("{");
for (j = 0; j < topSort[i].size()-1; j++)
printf("%d, ", topSort[i][j]);
printf("%d}
", topSort[i][j]);
}
return 0;
}
void Init()
{
scanf("%d", &vNum);
int u, v;
while (scanf("%d%d", &u, &v) != EOF)
{
G[u].push_back(v);
Gr[v].push_back(u); //反向
}
}
void DFS(int v)
{
visited[v] = true;
for (int i = 0; i < G[v].size(); i++)
{
if (!visited[G[v][i]])
DFS(G[v][i]);
}
node[counter++] = v; //后序遍历
}
void RDFS(int v, int k)
{
visited[v] = true;
topSort[k].push_back(v); //将属于同一强连通分量放一起
for (int i = 0; i < Gr[v].size(); i++)
{
if (!visited[Gr[v][i]])
RDFS(Gr[v][i], k);
}
}
int SCC()
{
memset(visited, false, sizeof(visited));
for (int v = 1; v <= vNum; v++)
{
if (!visited[v])
DFS(v);
}
memset(visited, false, sizeof(visited));
int k = 0; //初始化第一个强连通分量的拓扑序为1
for (int i = --counter; i >= 0; i--) //从编号最大开始
{
if (!visited[node[i]])
RDFS(node[i], k++);
}
return k;
}
测试运行结果:
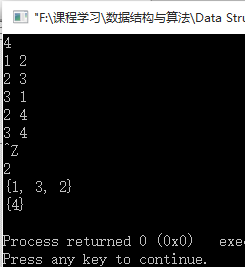
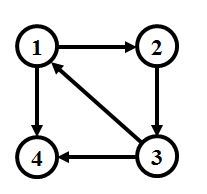
2. Tarjan算法
Tarjan算法和上文所说的双连通性问题的算法非常相似。它也是通过求出深度优先生成树的先序编号num[]和low[]。利用的性质是当num[v] == low[v]时,则以v为根节点的深度优先生成树中所有的节点为一个强连通分量,而为了获得强连通分量,我们需要用一个栈来记录。
Tarjan算法的伪码描述如下:
Tarjan(u)
{
num[u]=low[u] = counter //情况(1)
Stack.push(u) // 将节点u压入栈中
for each (u, v) in E // 枚举每一条边
if (v is not visted) // 如果节点v未被访问过
Tarjan(v) // 继续向下找
low[u] = min(low[u], low[v]) //情况(3)
else if (v in Stack) // 如果节点v还在栈内
Low[u] = min(low[u], num[v]) //情况(2)
if (num[u] == low[u]) // 如果节点u是强连通分量的根
repeat
v = Stack.pop // 将v退栈,为该强连通分量中一个顶点
print v
until (u== v)
}
c++代码:

/*
数据结构:邻接表存储图
*/
#include <cstdio>
#include <vector>
#include <algorithm>
#include <stack>
#include <cstring>
using namespace std;
const int MAX_N = 100;
vector<int> graph[MAX_N];
vector<int> topSort[MAX_N]; //下标为所属强分支的拓扑序
stack<int> scc;
int num[MAX_N], low[MAX_N];
int counter = 1;
int numSCC = 0; //强连通分量个数
int vNum; //顶点个数
bool inStack[MAX_N]; //判断顶点是否在栈中
bool visited[MAX_N];
void Init(); //初始化图
void Tarjan(int v); //tarjan算法查找SCC
void PrintSCC(); //打印所有SCC
void SCC();
int main()
{
Init();
SCC();
PrintSCC();
return 0;
}
void SCC()
{
memset(visited, false, sizeof(visited));
for (int i = 1; i <= vNum; i++)
{
if (!visited[i])
Tarjan(i);
}
}
void PrintSCC()
{
for (int i = 0; i < numSCC; i++)
{
int j;
printf("{");
for (j = 0; j < topSort[i].size() - 1; j++)
printf("%d, ", topSort[i][j]);
printf("%d}
", topSort[i][j]);
}
}
void Init()
{
int u, v;
scanf("%d", &vNum);
while (scanf("%d%d", &u, &v) != EOF)
{
graph[u].push_back(v);
}
}
void Tarjan(int v)
{
low[v] = num[v] = ++counter; //情况(1)
inStack[v] = true;
visited[v] = true;
scc.push(v);
for (int i = 0; i < graph[v].size(); i++)
{
int w = graph[v][i];
if (!visited[w])
{
Tarjan(w);
low[v] = min(low[v], low[w]); //情况(3)
}
else if (inStack[w])
{
low[v] = min(low[v], num[w]); //情况(2)
}
}
if (num[v] == low[v])
{
int w;
do
{
w = scc.top();
scc.pop();
inStack[w] = false;
topSort[numSCC].push_back(w);
} while (w != v);
numSCC++;
}
}
参考资料:《数据结构与算法分析-C语言描述》
《挑战程序设计竞赛》
博客:https://www.byvoid.com/blog/scc-tarjan/
