《剑指offer》---寻找反转数组最小值

本文算法使用python3实现

---

1.题目描述：

  把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。
  时间限制：3s；空间限制：32768K

---

2.思路描述：

  思路主要有以下两种：
  （1）暴力法：从头到尾遍历数组，找到最小值。该方法的时间复杂度为 $ O(n) $ ，当数组过大时，遍历时间较长，并且此方法并没有应用上“翻转数组”的特点。
  （2）折半查找法（二分查找）：时间复杂度为 $ O(log_2n) $ ，且可以利用本题“翻转”数组的特点。


  但是需要考虑两种情况!!!
  （1）存在重复数字，例如[1,0,1,1,1],使用暴力查找法，因为此时无法利用折半查找法里的一些判断条件。参考下图：
      

  （2）不存在重复数字，例如[3,4,5,1,2],使用折半查找法，参考下图：
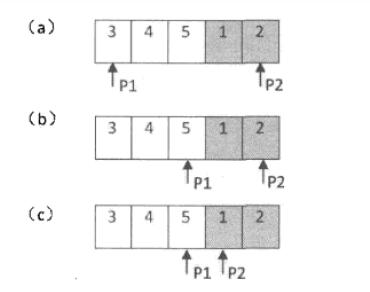
    （a）将指针 $ low $ 指向数组第0项， $ high $ 指向数组第n项。
    （b）指针 $ mid = (low+high)//2 $ ，若 $ array[mid]>=array[low] $ 且 $ array[mid]>array[high] $ ，此时移动指针 $ low=mid $ ；若 $ array[mid]<array[low] $ 且 $ array[mid]<=array[high] $ ，此时移动指针 $ high=mid $ 。重复(b)直到 $ low+1=high $ ，进入（c）
    （c）比较 $ array[low] $ 与 $ array[high] $ ，返回其中较小值。
      

---

3.程序代码：

class Solution:
    def minNumberInRotateArray(self, rotateArray):
        if len(rotateArray) == 0:
        	return 0
        #array = sorted(rotateArray)
        #return array[0]
        low = 0
        high = len(rotateArray) - 1
        while low + 1 < high:
        	mid = (low+high)//2
        	# 当数组为:[1,0,1,1,1]时，只能使用暴力解法
        	if rotateArray[mid] == rotateArray[low] and rotateArray[mid] == rotateArray[high]:
        		return self.findmin(rotateArray)
        	# 当数组正常时，例如:[3,4,5,1,2]，使用二分查找法。
        	# 注意等号：[3,0,1,1,1]，[3,3,3,0,1]这两种情况
        	if rotateArray[mid] >= rotateArray[low] and rotateArray[mid] > rotateArray[high]:
        		low = mid
        		continue
        	if rotateArray[mid] < rotateArray[low] and rotateArray[mid] <= rotateArray[high]:
        		high = mid
        		continue
        if low + 1 >= high:
        	return rotateArray[low] if rotateArray[low] < rotateArray[high] else rotateArray[high]

    def findmin(self,rotateArray):
        ''‘暴力解法’''
    	min = rotateArray[0]
    	for ele in rotateArray:
    		if ele < min:
    			min = ele
    	return min