浅谈树链剖分

※背景

1xxx年，一个月黑风高的夜晚，一位信息学界知名大佬正在修炼。忽然，他浑身金光大盛，搅动风云，天地失色。在那一片璀璨的金光中，有一算法应运而生。众大佬从四面八方看向这里，无不面色凝重。只听轰隆一声，宛若晴天霹雳，灵气翻腾，金光一闪，那神秘的算法不知所踪……

 

一、简介

以上就是树链剖分的诞生 （是我瞎编的

从它诞生时的天地异象就可以看出，此算法绝对不凡

那么树链剖分是个什么东西呢？

它是一个码量很大的可以实现树上各种操（xia）作（gao）的算法，比如可实现路径上的权值修改，子树的权值修改等

在学习树链剖分之前，必须先学习线段树，建议也掌握倍增求LCA

 

二、思想与一些概念

树链剖分的核心思想是：

将一棵树拆分成好多条互不相交的链，然后用数据结构（如线段树）去维护这些链

 

在一棵树中，有以下概念：

重儿子：一个非叶节点的所有儿子中，以这个儿子为根的子树中 节点数最多的子树 的那个儿子 为该节点的重儿子

换一个说法就是：定义size[x]为以x为根的子树的节点数（就是x和它的儿子孙子……的总数）。某节点的重儿子是它所有的儿子中size值最大的那一个

轻儿子：一个非叶节点除去重儿子的其它的儿子为轻儿子

重边：连接一个节点和它的重儿子的边为重边

轻边：不是重边的边为轻边

重链：几条连续的重边连接成一条链为重链

 

来一棵树

 

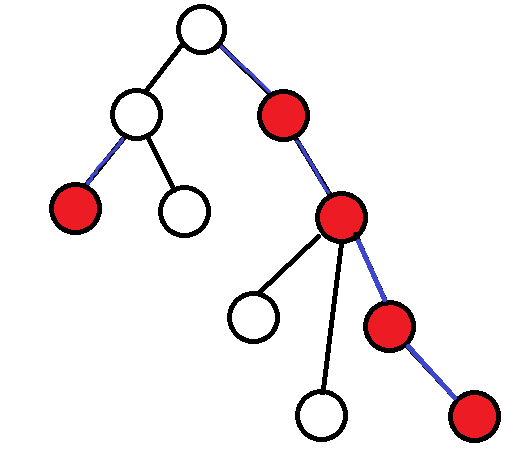
红色为重儿子，蓝色为重边，黑色为轻边。这棵树共有两条重链。

我们还可以发现以下结论：

1.重链的起点（如果不是根）是轻儿子

这也不难理解。如果这个起点是重儿子，那么它与它的父亲之间的边依然是重边，这条重边是重链的一部分，那么它就不是起点了，所以它一定是轻儿子

2.每一个轻儿子（包括根）都有一条以它为起点（为了方便理解，认为轻的叶子结点本身是一条重链）

如此一来，每一个节点都在重链上了，于是我们就可以把树拆成若干条重链，然后用线段树去维护

不过用线段树来维护重链有条件，那就是重链上的点的编号必须是连续的

那么该如何处理呢？

请往下看

 

三、步骤

（1）第一遍dfs

dfs1需要求出：

每个点的深度dep，每个点的父亲fa，以该点为根的子树的节点数siz（这个在上文提到过），每个点的重儿子son

这个应该没什么好说的，直接上代码：

void dfs1(int x,int f)//初始值x等于根节点
{
    dep[x]=dep[f]+1;//深度比它父亲大1
    fa[x]=f;//记录父亲
    siz[x]=1;//记录以它为根的子树节点个数
    int maxson=-1;
    for(int i=head[x];i;i=nxt[i])
    {
        int t=v[i];
        if(t==f) continue;
        dfs1(t,x);
        siz[x]+=siz[t];
        if(siz[t]>maxson)
        {
            son[x]=t;//更新重儿子
            maxson=siz[t];
        }
    }
}

 

（2）第二遍dfs

dfs2需要求出：

每个点的新编号id，新编号对应的值nw（可以不需要），每个点所在重链的起点top

上文说过，每条重链上面的节点编号都要是连续的，所以对于每个非叶节点，先遍历重儿子，然后遍历轻儿子

具体请看代码：

void dfs2(int x,int topx)//topx为重链的起点
{
    id[x]=++cnt;//新编号（满足重链上的编号是连续的）
    nw[id[x]]=w[x];//新编号对应的值（可以不需要，用w[id[x]]代替）
    top[x]=topx;//重链的起点
    if(!son[x]) return;//叶子结点的情况
    dfs2(son[x],topx);//先遍历重儿子（重儿子与当前节点在同一条重链上，所以topx不变）
    for(int i=head[x];i;i=nxt[i])
    {
        int t=v[i];
        if(t==fa[x] || t==son[x]) continue;
        dfs2(t,t);//每个轻儿子都有一条以自己为起点的重链
    } 
}

 

（3）路径权值修改

步骤如下：

1.若两个节点x,y不在一条重链上，比较dep[top[x]]与dep[top[y]]，选择较大为x（即重链起点较深的一个，原因不难想）

2.top[x]一定在x到y的路径上，而x与top[x]在一条重链上，节点编号连续，所以用线段树处理

3.修改x为fa[top[x]]。重复以上操作，直到x和y在一条重链上

4.此时x与y的路径编号连续，用线段树处理

这个过程与倍增求LCA的思想有点类似

具体请看代码：

void upadd(int x,int y,int num)
{
    num%=MOD;//视题目要求而定
    while(top[x]!=top[y])//两个节点不在一条重链上
    {
        if(dep[top[x]]<dep[top[y]])//步骤1，选择重链的起点较深的一个点向上走
            swap(x,y);
        qadd(1,n,1,id[top[x]],id[x],num);//步骤2，用线段树处理这条重链
        x=fa[top[x]];//步骤3，x到了另一条重链上
    }
    if(dep[x]>dep[y])
        swap(x,y);
    qadd(1,n,1,id[x],id[y],num);// 步骤4，x和y在一条重链上了，直接用线段树处理
}

 

路径权值求和同理，只是把线段树的区间修改变为区间查询

int upfind(int x,int y)
{
    int ans=0;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])
            swap(x,y);
        ans=(ans+qfind(1,n,1,id[top[x]],id[x]))%MOD;
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])
        swap(x,y);
    ans=(ans+qfind(1,n,1,id[x],id[y]))%MOD;
    return ans;
}

 

（4）子树权值修改

任何一颗子树的节点编号也都是连续的，设根为x，则编号为id[x]~id[x]+siz[x]-1，所以直接用线段树处理，简单粗暴

什么？一颗子树节点编号为什么是连续的？

因为处理编号时用的是dfs啊~

代码如下：

void downadd(int x,int num)
{
    num%=MOD;//视题目要求而定
    qadd(1,n,1,id[x],id[x]+siz[x]-1,num);
}

 

子树权值查询同理：

int downfind(int x)
{   
    return qfind(1,n,1,id[x],id[x]+siz[x]-1);
}

 

---

 

 

下面看一道模板题

洛谷P3384

 

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cmath>
#define MAXN 200005
using namespace std;

inline int read()
{
    int f=1,x=0;
    char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-') f=-1; ch=getchar();}
    while(ch>='0' && ch<='9') {x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}

int n,m,root,MOD;
int cnt;
int w[MAXN];
int v[MAXN<<1],head[MAXN],nxt[MAXN<<1];
int dep[MAXN],fa[MAXN],son[MAXN],siz[MAXN];
int id[MAXN],nw[MAXN],top[MAXN];
int segtree[MAXN<<2],lazytag[MAXN<<2];

void add(int x,int y)
{
    v[++cnt]=y;
    nxt[cnt]=head[x];
    head[x]=cnt;
}

void build(int l,int r,int num)
{
    if(l==r)
    {
        segtree[num]=nw[l]%MOD;
        return ;
    }
    int mid=(l+r)/2;
    build(l,mid,num<<1);
    build(mid+1,r,(num<<1)|1);
    segtree[num]=(segtree[num<<1]+segtree[(num<<1)|1])%MOD;
}

void vadd(int l,int r,int num,int val)
{
    lazytag[num]+=val;
    segtree[num]+=((r-l+1)%MOD)*(val%MOD);
    lazytag[num]%=MOD;
    segtree[num]%=MOD;
}

void lazydown(int l,int r,int num,int mid)
{
    if(!lazytag[num]) return ;
    vadd(l,mid,num<<1,lazytag[num]);
    vadd(mid+1,r,(num<<1)|1,lazytag[num]);
    lazytag[num]=0;
} 

void qadd(int l,int r,int num,int ll,int rr,int val)
{
    if(ll<=l && r<=rr)
    {
        vadd(l,r,num,val);
        return ;
    }
    int mid=(l+r)/2;
    lazydown(l,r,num,mid);
    if(ll<=mid)
        qadd(l,mid,num<<1,ll,rr,val);
    if(mid<rr)
        qadd(mid+1,r,(num<<1)|1,ll,rr,val);
    segtree[num]=(segtree[num<<1]+segtree[(num<<1)|1])%MOD;
}

int qfind(int l,int r,int num,int ll,int rr)
{
    if(ll<=l && r<=rr)
    {
        return segtree[num]%MOD;
    }
    int mid=(l+r)/2,ans=0;
    lazydown(l,r,num,mid);
    if(ll<=mid)
        ans+=qfind(l,mid,num<<1,ll,rr);
    if(mid<rr)
        ans+=qfind(mid+1,r,(num<<1)|1,ll,rr);
    return ans%MOD;
}

void dfs1(int x,int f)
{
    dep[x]=dep[f]+1;
    fa[x]=f;
    siz[x]=1;
    int maxson=-1;
    for(int i=head[x];i;i=nxt[i])
    {
        int t=v[i];
        if(t==f) continue;
        dfs1(t,x);
        siz[x]+=siz[t];
        if(siz[t]>maxson)
        {
            son[x]=t;
            maxson=siz[t];
        }
    }
}

void dfs2(int x,int topx)
{
    id[x]=++cnt;
    nw[id[x]]=w[x];
    top[x]=topx;
    if(!son[x]) return;
    dfs2(son[x],topx);
    for(int i=head[x];i;i=nxt[i])
    {
        int t=v[i];
        if(t==fa[x] || t==son[x]) continue;
        dfs2(t,t);
    } 
}

void upadd(int x,int y,int num)
{
    num%=MOD;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])
            swap(x,y);
        qadd(1,n,1,id[top[x]],id[x],num);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])
        swap(x,y);
    qadd(1,n,1,id[x],id[y],num);
}

int upfind(int x,int y)
{
    int ans=0;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])
            swap(x,y);
        ans=(ans+qfind(1,n,1,id[top[x]],id[x]))%MOD;
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])
        swap(x,y);
    ans=(ans+qfind(1,n,1,id[x],id[y]))%MOD;
    return ans;
}

void downadd(int x,int num)
{
    num%=MOD;
    qadd(1,n,1,id[x],id[x]+siz[x]-1,num);
}

int downfind(int x)
{   
    return qfind(1,n,1,id[x],id[x]+siz[x]-1);
}

int main()
{
    int i;
    int h,a,b,c;
    n=read(); m=read(); root=read(); MOD=read();
    for(i=1;i<=n;i++) w[i]=read();
    for(i=1;i<n;i++)
    {
        a=read();
        b=read();
        add(a,b);
        add(b,a);
    }
    dfs1(root,0);
    cnt=0;
    dfs2(root,root);
    build(1,n,1);
    for(i=1;i<=m;i++)
    {
        h=read();
        if(h==1)
        {
            a=read(); b=read(); c=read();
            upadd(a,b,c);
        }
        if(h==2)
        {
            a=read(); b=read();
            printf("%d
",upfind(a,b));
        }
        if(h==3)
        {
            a=read(); b=read();
            downadd(a,b);
        }
        if(h==4)
        { 
            a=read();
            printf("%d
",downfind(a));
        }
    }
    return 0;
}

 

最后，提醒您：

树剖千万行，认真第一行

代码不规范，测评两行WA