(传说,在神秘的初赛中,选手们经常互相爆零以示友好……)
历年真题:ti.luogu.com.cn
以下标题中打*的是我认为的重点内容
一、关于计算机
(一)计算机组成
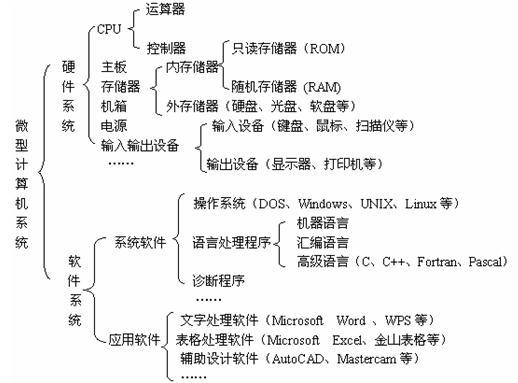
硬件组成:
1. 控制器(Control):是整个计算机的中枢神经,其功能是对程序规定的控制信息进行解释,根据其要求进行控制,调度程序、数据、地址,协调计算机各部分工作及内存与外设的访问等。
2. 运算器(Datapath):运算器的功能是对数据进行各种算术运算和逻辑运算,即对数据进行加工处理。
3. 存储器(Memory):存储器的功能是存储程序、数据和各种信号、命令等信息,并在需要时提供这些信息。
4. 输入(Input system):输入设备是计算机的重要组成部分,输入设备与输出设备合称为外部设备,简称外设,输入设备的作用是将程序、原始数据、文字、字符、控制命令或现场采集的数据等信息输入到计算机。常见的输入设备有键盘、鼠标器、光电输入机、磁带机、磁盘机、光盘机等。
5. 输出(Output system):输出设备与输入设备同样是计算机的重要组成部分,它把外算机的中间结果或最后结果、机内的各种数据符号及文字或各种控制信号等信息输出出来。微机常用的输出设备有显示终端CRT、打印机、激光印字机、绘图仪及磁带、光盘机等。
【CPU(中央处理器)=运算器+控制器+寄存器
存储器=内存储器+外存储器】
BIOS是英文"Basic Input Output System"的缩略语,直译过来后中文名称就是"基本输入输出系统"。其实,它是一组固化到计算机内主板上一个ROM芯片上的程序,它保存着计算机最重要的基本输入输出的程序、系统设置信息、开机后自检程序和系统自启动程序。 其主要功能是为计算机提供最底层的、最直接的硬件设置和控制。
随机存储器RAM的“随机”指“随时访问”
断电后可以保存数据:硬盘,ROM
断电后不可以保存数据:显存(显卡内存),RAM,CPU
面向过程语言 :C
面对对象的高级语言:C++,Java
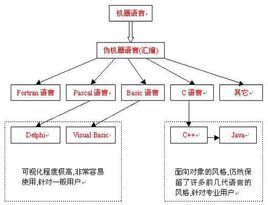
(二)计算机发展史
(这部分中部分内容参考洛谷日报第45期。感谢)

(三)计算机中各存储单位的进位关系:
1TB=1024GB,1GB=1024MB,1MB=1024KB
1KB=1024B,1B(字节)=8bit(位)
二、二进制原码、反码与补码
(这部分中部分内容参考https://blog.csdn.net/jq_ak47/article/details/45338061。感谢)
(一)原码
在计算机中(以八位机为例),我们知道都用二进制来存储数
如5,二进制为00000101
那么负数怎么存储?将最高位设为符号位,正数为0,负数为1
如-5,二进制为10000101
-6,为10000110
以上叫做原码
(二)反码
反码表示法规定:正数的反码与其原码相同;负数的反码是对其原码逐位取反,但符号位除外。
如7,原码为00000111,反码为00000111
如-10,原码为10001010,反码为11110101
(三)补码
正数的补码是其本身,负数的补码是反码加一
补码有什么用呢?解决负整数加减法
比如我们计算16-8 或是 16+(-8)
如果用原码计算
0 0 0 0 1 0 0 0
+1 0 0 0 0 1 0 0
————————
1 0 0 0 1 1 1 1
将10001111转换为二进制,结果为-24,显然不对
如果用补码呢?
0 0 0 0 1 0 0 0
+ 1 1 1 1 1 1 0 0
————————
1 0 0 0 0 0 1 0 0
*注意,此处用八位二进制,而计算结果是九位二进制,所以最高位自动省略
这样结果是-8,正确
若要将补码转化为原码,正数不变,负数先-1再取反码就可以了
三、P问题、NP问题与NPC问题
(这部分中部分内容参考http://www.matrix67.com/blog/archives/105。感谢)
我就说的简略一点了(主要是怕自己忘了),详见上面网址
(一)P问题
每个问题的算法都有时间复杂度
O(1),O(N),O(NlogN),O(n2)等n不在指数为的复杂度为多项式级复杂度
O(N!),O(2n)等复杂度是非多项式级的
可以找到一个多项式级复杂度算法的问题是P问题
NOI系列考的绝大多数问题都是P问题
注:如果一个问题不存在多项式空间的算法,那它一定不是 P 类问题(详见NOIP2012提高组初赛第20题)
(二)NP问题
一个解可以用多项式级复杂度检验的问题是NP问题
注:找不到多项式复杂度解的(非P问题)不一定是NP问题
易得NP=P。即所有P问题都是NP问题
至于P=NP,大家感兴趣的话可以自己研究研究(滑稽护体)
(三)NPC问题(NP-完全问题)
先讲一下“约化”
有两个问题,问题A和问题B
若可以用问题B的算法来解决问题A,那么问题A可以约化为问题B
比如,一元一次方程可以约化为一元二次方程
约化具有传递性,即A可以约化成B,B可以约化成C,那么A一定可以约化成C
可以看出,在不断约化的过程中,算法的时间复杂度逐渐增高,解决的问题也越来越广
大胆猜测,是否可以将所有的NP问题都约化成一个问题?解决了这个问题就能解决所有NP问题?
答案是肯定的!
而且这不仅是一个问题,还是一类问题
这类问题叫做NPC问题。
一个问题满足以下两条,它就是NPC问题:
1、它是NP问题
2、所有的NP问题都可以约化到它
NPC问题的鼻祖是逻辑电路问题,有兴趣的读者可以自行了解。
另外说一下NP-hard问题,它满足NPC问题的第二条但不满足第一条。它的范围比NPC问题广。
*四、进制转换
(一)二、四、八、十六互转通用方法:
以八进制转二进制为例
先把关系表列出来:
|
八进制数 |
二进制数 |
|
0 |
000 |
|
1 |
001 |
|
2 |
010 |
|
3 |
011 |
|
4 |
100 |
|
5 |
101 |
|
6 |
110 |
|
7 |
111 |
二转八:
例如:10010011.1011
2^3=8
所以使用三位一合的方法。若整数部分位数不是三的倍数,在最高位前补0;若小数部分位数不是三的倍数,在末尾补0。接着以小数点为分界,从左到右分别转化小数部分和整数部分。
对照上面的表 10 010 011. 101 100
2 2 3 . 5 4
所以(10010011.1011)2=(223.54)8
八转二:
同理,一位三分法
例如:7643
对照上面的表 7 6 4 3
111 110 100 011
注:十六进制等进制中,A代表10,B代表11,以此类推
(二) 二转十和十转二
二转十:个位*2^0,十位*2^1,百位*2^2…… 若是小数,十分位*2^-1,百分位*2^-2……然后加起来就行了
十转二:整数部分:不断除以2,直到商为0,倒取各阶段余数
小数部分:不断乘以2,直到积为1,正取各阶段整数
如10.25转化为二进制
10÷2=5……0
5÷2=2……1
2÷2=1……0
1÷2=0……1
倒着取余数,1010即为整数部分
0.25*2=0.5……0
0.5*2=1……1
正着取整数,0.01即为小数部分
将两部分合起来,得到10.25=(1010.01)2
(三)其它
其它2^n的进制如要转化为十进制,先转化为二进制,再转化为十进制。
十进制转化成它们同理。
**五、排序算法
基本是每年必考!
(这部分中部分内容参考http://blog.csdn.net/whuslei/article/details/6442755/ 和 https://blog.csdn.net/xiazdong/article/details/8462393。感谢)
九大排序算法:(加上桶排序就是十个)
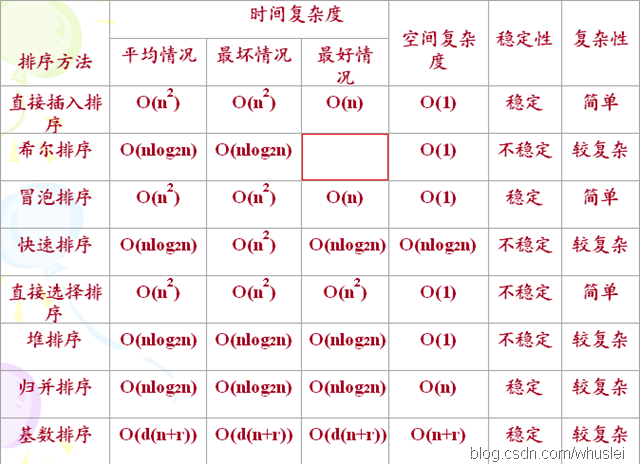
计数排序 O(N+K) O(N+K) O(N+K) O(n+K) 稳定 简单
排序算法稳定,指排序前后数值相同的两个数相对位置不会改变
稳定:插、归、冒、基、计
不稳定:快、堆、希、选
需要额外空间:归、基、计
不需要额外空间:插、希、冒、快、堆、选
运用分治思想的:归、快
时间复杂度是O(NlogN)的:堆、快、归(希尔排序的时间复杂度依赖于增量的选择,这里不做讨论)
最慢是O(N2)的:插、冒、快、选
最快是O(N)的:插、冒(改进后)
最快最慢相同的:冒(不改进)、选、堆、归、基,计
注意:近些年题目考的越来越“活”了,千万不要死记硬背!
example:(NOIP2017提高组)
11.设 A 和 B 是两个长为 n 的有序数组,现在需要将 A 和 B 合并成一个排好序的 数组,请问任何以元素比较作为基本运算的归并算法最坏情况下至少要做 ( )次比较。
[黑人问号.jpg]
答案:2n-1
六、时空复杂度
(一)时间复杂度
(这部分中部分内容参考https://www.luogu.org/blog/Chanis/master。感谢 )
表的第二行是一些奇怪的东西,不用管它
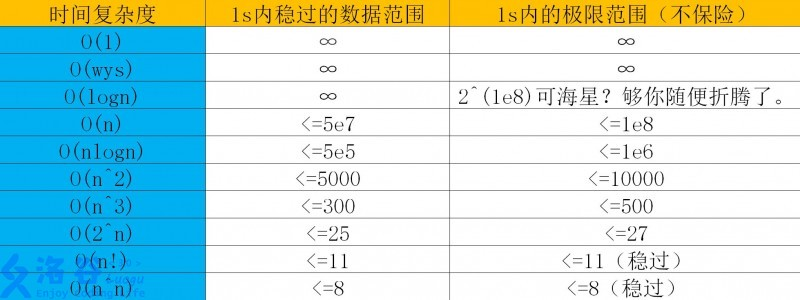
初赛还经常要计算代码的时间复杂度。对于递归函数的一定要细心思考
(二)空间复杂度
(这部分中部分内容参考https://blog.csdn.net/shiwei408/article/details/7280296?utm_source=copy 。感谢)
32位系统下,int、long、long long、__int64所占字节数(B)
char: 1字节(8位)
int: 4字节 (32位,取值范围 -2^31 ~ 2^31-1)
unsigned int : 4字节 (32位,取值范围 0 ~ 2^32-1)
long: 4字节 (32位,取值范围 -2^31 ~ 2^31-1)
unsigned long : 4字节 (32位,取值范围 0 ~ 2^32-1)
long long : 8字节(64位,取值范围 -2^63 ~ 2^63-1)
七、位运算与逻辑运算
(一)位运算
按位与:&
按位或:|
按位异或:^
按位取反:~(对于十进制来说,取相反数再减一)
左移:<<
右移:>>
*优先级:~大于>>、<<大于&大于^大于|大于&=、^=、|=、<<=、>>=
(二)逻辑运算
"∨" 表示"或" (逻辑加法)
"∧" 表示"与". (逻辑乘法)
"┐"表示"非". (逻辑否定)
"⊕"表示"异或"
按位运算优先级大于逻辑运算
与:11为1,其它为0
或:00为0,其它为1
异或:不同为1,相同为0
八、指针
一个小东西……不过易混淆!
int a;//定义一个变量
int *p;//定义一个指针
*p=&a;//指针p取到a的地址(p是一个地址)
cout<<*p;//输出地址中的值(*p是一个值)
example:NOIP2015提高组第24题
#include <iostream> using namespace std; void fun(char *a, char *b) { a = b; //a变为c2的地址。注意,指针=指针时地址中的值不变,变的只是指针 (*a)++; //将a地址(c2)中的值+1 } int main() { char c1, c2, *p1, *p2; c1 = 'A'; c2 = 'a'; p1 = &c1; //p1是c1的地址 p2 = &c2; //p2是c2的地址 fun(p1, p2); //(NOIP的函数好像都叫fun……) cout << c1 << c2 << endl;//输出为Ab return 0; }
*九、图论(只讲一点点)
图论挺重要的,板子需要背一背
下面只是一些概念
(一)无向图
完全图:n 个点,n(n-1)/2 条边(每对顶点之间都恰连有一条边)
树:n 个点,n-1 条边(每对顶点之间都有且仅有一条路径,无环)
割点:删除该点后图不连通
割边(桥):删除该边后图不连通
点双连通:某个没有割点的无向图
边双连通:某个没有割边(桥)的无向图
双连通分量:图的极大双连通子图(分为点双连通分量和边双联通分量)
(二)有向图
强连通:在有向图G中,若u能到v,v也能到u,则称u和v是强连通的
强连通图:若有向图G的任意两个节点都强连通,则称G是一个强连通图
强连通分量:有向非强连通图的极大强连通子图,称为强连通分量
DAG:有向无环图
将一个有向图中的强连通分量都缩成一个点,则原图会形成一个DAG
拓扑排序仅适用于DAG
十、计算机奖项
(这部分中部分内容参考https://blog.csdn.net/qq_39992190/article/details/78160251?utm_source=copy。感谢)
图灵奖 (A.M. Turing Award) 由ACM于1966年设立
“计算机界的诺贝尔奖”
奖励那些对计算机事业做出重要贡献的个人
约翰•冯•诺依曼奖 由IEEE(电气和电子工程师协会)于1990年成立
表扬在计算机科学和技术上具有杰出成就的科学家
高德纳奖 (Donald E. Knuth Prize) 始于1996 1.5年颁发一次
授予为计算机科学基础做出杰出贡献的人
……
二一四七四八三六四七、一些杂乱的
(一)根据国际信息学奥林匹克竞赛(IOI)的相关决议并考虑到我国目前程序设计语言的具体情况,CCF决定:1.2020年开始,除NOIP以外的NOI系列其他赛事(包括冬令营、CTSC、APIO、NOI)将不再支持Pascal语言和C语言;2.从2022年开始,NOIP竞赛也将不再支持Pascal语言。即从NOIP2022开始,NOI系列的所有赛事将全部取消Pascal语言。在无新增程序设计语言的情况下,NOI系列赛事自NOIP2022开始将仅支持C++语言。(NOIP2017提高组第一题)
(二)IP地址是一个32位的二进制数,通常被分割为4个“8位二进制数”(也就是4个字节)。IP地址通常用“点分十进制”表示成(a.b.c.d)的形式,其中,a,b,c,d都是0~255之间的十进制整数。例:点分十进IP地址(100.4.5.6),实际上是32位二进制数(01100100.00000100.00000101.00000110)。
(三)哈夫曼编码采用贪心思想。该方法完全依据字符出现概率来构造异字头的平均长度最短的码字。哈夫曼树的叶子节点个数比非叶子节点个数多一。
(四)编译器的主要功能是将源程序翻译成指令
(五)字串是连续的,但子序列不一定是连续的

祝所有参赛选手rp++,score++,luck++!!!
本文部分图片来源于网络
若需转载,请注明https://www.cnblogs.com/llllllpppppp/p/9749930.html