2-3树
我们在二叉查找树中曾介绍过二叉查找树有可能会出现最坏的情况,所有的结点变成了一条链。如图

我们当然希望我们能保存二叉查找树的平衡性,但是在动态插入过程中保证树的完美平衡代价太大了。我们退而求其次,学习一种新的数据结构。
相关定义:
2-结点:含有一个键(及对应值)和两条链接,左链接指向2-3树中的键都小于该结点,右链接指向2-3树中的键都大于该结点。
3-结点:含有两个键(及对应的值)和三条链接,左链接指向2-3树中的键都小于该结点,中链接指向的2-3树中的键都位于该结点的两个键之间,右链接指向2-3树中的键都大于该结点。
如图

一颗完美的2-3查找树中所有的空链接到根结点的距离都是相等的
查找
首先我们将一个键与根结点中的键比较,如果他和其中任意一个相等,则命中;否则就根据比较的结果找到指向相应区域的链接,并在其指向的子树中继续查找。如果是空链接,则查找未命中。
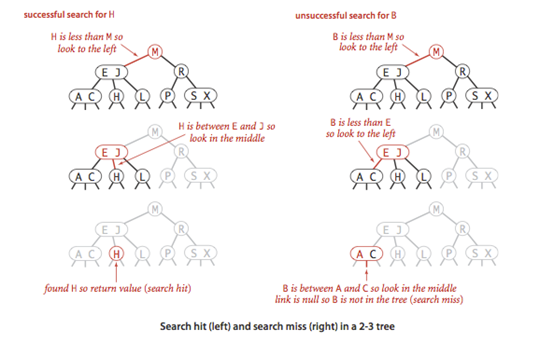
对于左边的查找情况,我们查找H,发现他h<m,所以就在M的左子树中继续查找,H在E和J之间,所以我们在中子树继续查找,命中
对于右边的情况,我们查找B,发现B<M,,就在M的左子树中继续查找,发现B<E,就在的左子树中继续查找,发现B在A和C中间,查找它们的中子树为空,未命中。
插入
我们分为4中情况讨论
向2-结点中插入新键
我们只需要把这个2-结点替换为一个3-结点即可。如图,插入K
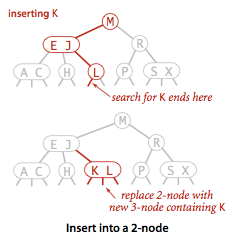
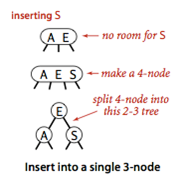
向一颗只含有一个3-结点的树中插入新键。
在考虑一般情况之前,我们先考虑这样一种情况,一棵树只有一个3-结点,现在我们往里插入新键,使它暂时变为一个4-结点,而一个4结点可以很方便的转化为含有3个2-结点的2-3树,只不过树高增加了1而已。这三个结点其中一个(跟)含有中键,一个结点含有3个键中的最小者(左链接),一个含有最大者(右链接)
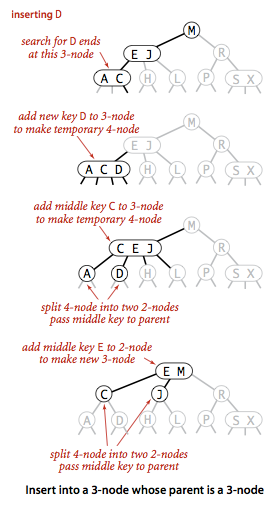
向一个父节点为2-结点的3-结点插入新键
我们先构建出一个临时的4-结点并将其分解,但是我们不会为中键创建一个新结点,而是将他移动到原来的父结点中。即将原来指向3-结点的链接替换为新父结点中的原中键左右两边的两条链接。,这种转化不影响2-32树的主要性质

向一个父结点为3-结点的3-结点插入新键
我们和刚才一样构造一颗临时的4-结点然后分解他,将他的中间插入到父结点中,但是父结点也是一个3-结点,因此我们继续构造一个临时的4-结点,继续进行相同的变换。以此类推,直到遇到一个2-结点或者到达3-结点的根
分解根结点
如果从插入结点到根结点的路径上全是3-结点,我们的根结点就变成了一个临时的4-结点,此时我们可以按照向一颗只含有一个3-结点的树中插入新键的方法处理,将树高加1.这次变换仍然保持了树的性质

全局性质
上面介绍的变换不会影响树的全局有序性和平衡性,任意空链接到根结点的距离都是相等的