转：完整的最简单的谱聚类python代码

http://blog.csdn.net/waleking/article/details/7584084

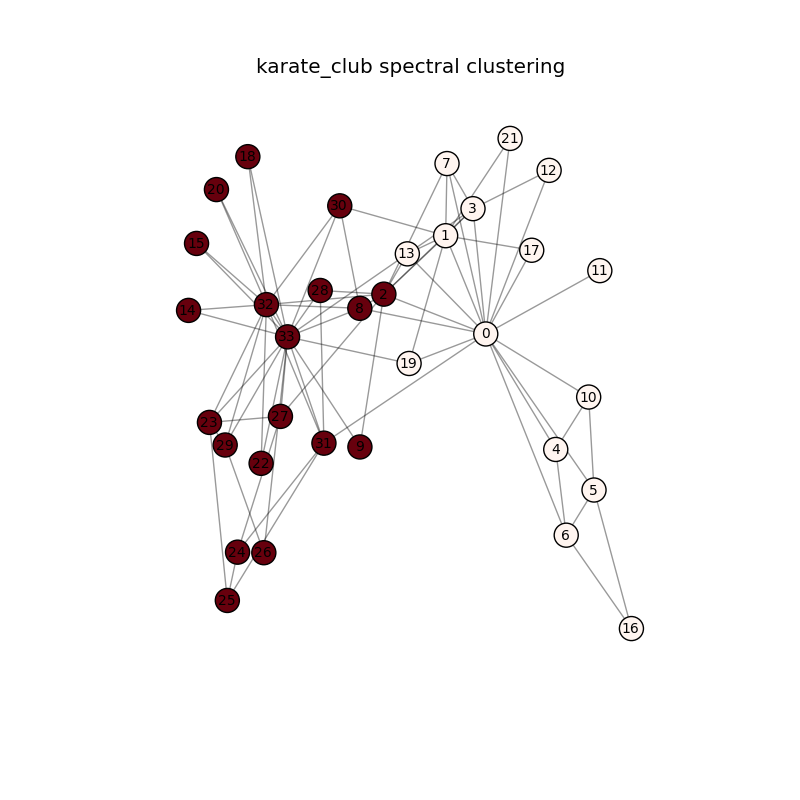
针对karate_club数据集，做了谱聚类。由于是2-way clustering，比较简单，得到了图的新的表示空间之后，没有做k-means，仅仅针对正规化后的拉普拉斯矩阵的第二特征值做了符号判断，这和Spectral Clustering Tutorial 一文中的描述一致。

引用了numpy scipy matplotlib networkx包

1.  
   #coding=utf-8
2.  
   #MSC means Multiple Spectral Clustering
3.  
   import numpy as np
4.  
   import scipy as sp
5.  
   import scipy.linalg as linalg
6.  
   import networkx as nx
7.  
   import matplotlib.pyplot as plt
8.  
    
9.  
   def getNormLaplacian(W):
10.  
    """input matrix W=(w_ij)
11.  
    "compute D=diag(d1,...dn)
12.  
    "and L=D-W
13.  
    "and Lbar=D^(-1/2)LD^(-1/2)
14.  
    "return Lbar
15.  
    """
16.  
    d=[np.sum(row) for row in W]
17.  
    D=np.diag(d)
18.  
    L=D-W
19.  
    #Dn=D^(-1/2)
20.  
    Dn=np.power(np.linalg.matrix_power(D,-1),0.5)
21.  
    Lbar=np.dot(np.dot(Dn,L),Dn)
22.  
    return Lbar
23.  
     
24.  
    def getKSmallestEigVec(Lbar,k):
25.  
    """input
26.  
    "matrix Lbar and k
27.  
    "return
28.  
    "k smallest eigen values and their corresponding eigen vectors
29.  
    """
30.  
    eigval,eigvec=linalg.eig(Lbar)
31.  
    dim=len(eigval)
32.  
     
33.  
    #查找前k小的eigval
34.  
    dictEigval=dict(zip(eigval,range(0,dim)))
35.  
    kEig=np.sort(eigval)[0:k]
36.  
    ix=[dictEigval[k] for k in kEig]
37.  
    return eigval[ix],eigvec[:,ix]
38.  
     
39.  
    def checkResult(Lbar,eigvec,eigval,k):
40.  
    """
41.  
    "input
42.  
    "matrix Lbar and k eig values and k eig vectors
43.  
    "print norm(Lbar*eigvec[:,i]-lamda[i]*eigvec[:,i])
44.  
    """
45.  
    check=[np.dot(Lbar,eigvec[:,i])-eigval[i]*eigvec[:,i] for i in range(0,k)]
46.  
    length=[np.linalg.norm(e) for e in check]/np.spacing(1)
47.  
    print("Lbar*v-lamda*v are %s*%s" % (length,np.spacing(1)))
48.  
     
49.  
    g=nx.karate_club_graph()
50.  
    nodeNum=len(g.nodes())
51.  
    m=nx.to_numpy_matrix(g)
52.  
    Lbar=getNormLaplacian(m)
53.  
    k=2
54.  
    kEigVal,kEigVec=getKSmallestEigVec(Lbar,k)
55.  
    print("k eig val are %s" % kEigVal)
56.  
    print("k eig vec are %s" % kEigVec)
57.  
    checkResult(Lbar,kEigVec,kEigVal,k)
58.  
     
59.  
    #跳过k means，用最简单的符号判别的方法来求点的归属
60.  
     
61.  
    clusterA=[i for i in range(0,nodeNum) if kEigVec[i,1]>0]
62.  
    clusterB=[i for i in range(0,nodeNum) if kEigVec[i,1]<0]
63.  
     
64.  
    #draw graph
65.  
    colList=dict.fromkeys(g.nodes())
66.  
    for node,score in colList.items():
67.  
    if node in clusterA:
68.  
    colList[node]=0
69.  
    else:
70.  
    colList[node]=0.6
71.  
    plt.figure(figsize=(8,8))
72.  
    pos=nx.spring_layout(g)
73.  
    nx.draw_networkx_edges(g,pos,alpha=0.4)
74.  
    nx.draw_networkx_nodes(g,pos,nodelist=colList.keys(),
75.  
    node_color=colList.values(),
76.  
    cmap=plt.cm.Reds_r)
77.  
    nx.draw_networkx_labels(g,pos,font_size=10,font_family='sans-serif')
78.  
    plt.axis('off')
79.  
    plt.title("karate_club spectral clustering")
80.  
    plt.savefig("spectral_clustering_result.png")
81.  
    plt.show()

所得聚类结果：

感谢python社区！

life is short, use python!