CF div2 320 D

D. "Or" Game

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given n numbers a1, a2, ..., an. You can perform at most k operations. For each operation you can multiply one of the numbers by x. We want to make 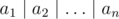 as large as possible, where  denotes the bitwise OR.

Find the maximum possible value of 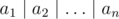 after performing at most k operations optimally.

Input

The first line contains three integers n, k and x (1 ≤ n ≤ 200 000, 1 ≤ k ≤ 10, 2 ≤ x ≤ 8).

The second line contains n integers a1, a2, ..., an (0 ≤ ai ≤ 109).

Output

Output the maximum value of a bitwise OR of sequence elements after performing operations.

Sample test(s)

input

3 1 2
1 1 1

output

3

input

4 2 3
1 2 4 8

output

79

Note

For the first sample, any possible choice of doing one operation will result the same three numbers 1, 1, 2 so the result is .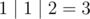

For the second sample if we multiply 8 by 3 two times we'll get 72. In this case the numbers will become 1, 2, 4, 72 so the OR value will be 79 and is the largest possible result.

 题目意思是求一组数的或值最大，其中的元素可以乘k次x 问最大值是多少。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
#include <stack>

using namespace std;

const int M = 10005;
const int maxn = 5000000;
typedef long long ll;

vector<int>G[maxn];
queue<int>Q;
stack<int>st;


long long a[maxn];
long long suml[maxn];
long long sumr[maxn];

int main()
{
   int n,k,x;
   scanf("%d%d%d",&n,&k,&x);
   int t = 1;
   while(k--){
    t *= x;
   }
   for(int i=1;i<=n;i++){
    scanf("%lld",&a[i]);

   }
   //suml[1] = a[1];
   for(int i=1;i<=n;i++){
    suml[i] = suml[i-1]|a[i];
   }
   //sumr[n] = a[n];
   for(int i=n;i>0;i--){
    sumr[i] = sumr[i+1]|a[i];
   }
   long long ans = 0;
   for(int i=1;i<=n;i++){
    ans = max(ans,suml[i-1]|(a[i]*t)|sumr[i+1]);
   }
   printf("%lld
",ans);

    return 0;
}