SegmentTree

解决区间求最大最小值 区间和问题 朴素暴力方法时间复杂度为O(n) 而这种方法可以使复杂度降低为O(logn)

数组元素 存在叶子节点  {1, 3, 5, 7, 9, 11}

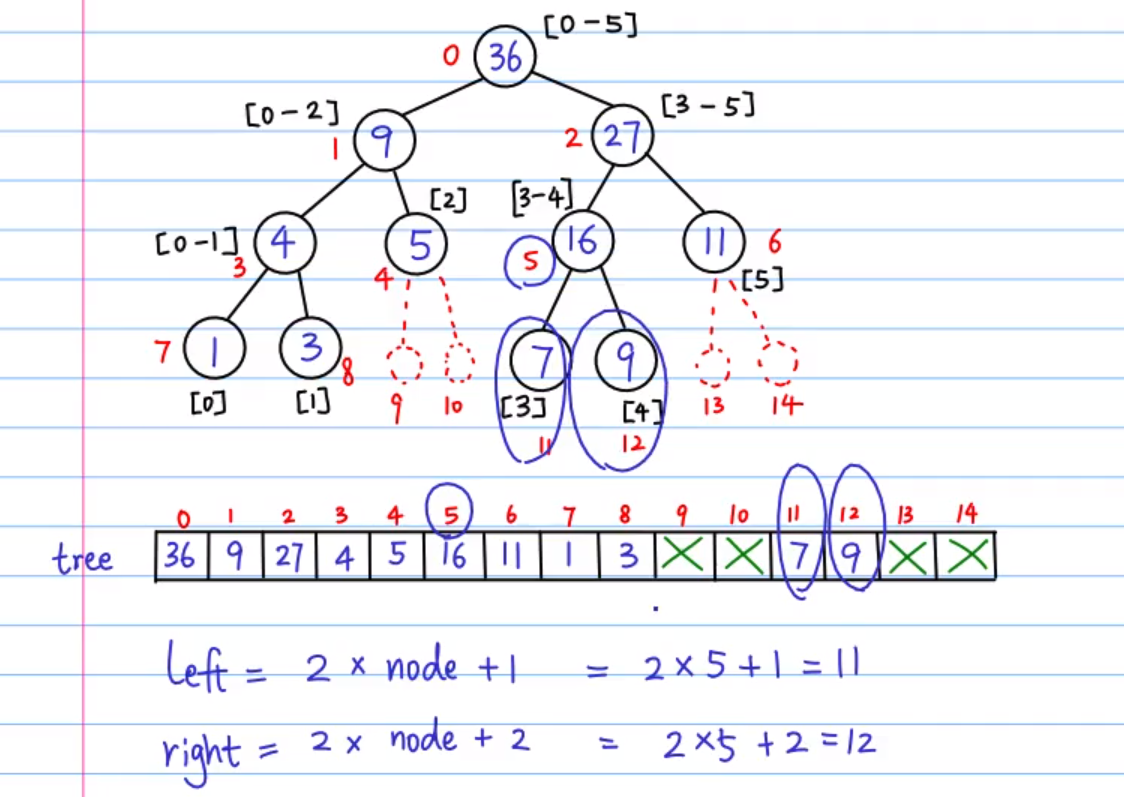
public class SegmentTree {
    private static int[] arr = {1, 3, 5, 7, 9, 11};
    private static int size = arr.length;
    private static int[] tree = new int[4 * size];

    private void build_tree(int node, int start, int end) {
        System.out.printf("node:%d start:%d end:%d
", node, start, end);
        if (start == end) {
            tree[node] = arr[start];
        } else {
            int mid = (start + end) / 2;
            int left_node = 2 * node + 1;
            int right_node = 2 * node + 2;

            build_tree(left_node, start, mid);
            build_tree(right_node, mid + 1, end);

            tree[node] = tree[left_node] + tree[right_node];
        }
    }

    private void update_tree(int node, int start, int end, int idx, int val) {
        if (start == end) {
            arr[idx] = val;
            tree[node] = val;
        } else {
            int mid = (start + end) / 2;
            int left_node = 2 * node + 1;
            int right_node = 2 * node + 2;

            if (idx >= start && idx <= mid) {
                update_tree(left_node, start, mid, idx, val);
            } else {
                update_tree(left_node, mid + 1, end, idx, val);
            }

            tree[node] = tree[left_node] + tree[right_node];
        }
    }

    private int query_tree(int node, int start, int end, int L, int R) {
        if (R < start || L > end) {
            return 0;
        }else if(L <= start && end <= R){
            return tree[node];
        } else if (start == end) {
            return tree[node];
        } else {
            int mid = (start + end) / 2;
            int left_node = 2 * node + 1;
            int right_node = 2 * node + 2;

            int sum_left = query_tree(left_node, start, mid, L, R);
            int right_left = query_tree(right_node, mid + 1, end, L, R);

            return sum_left + right_left;
        }
    }


    public static void main(String[] args) {
        new SegmentTree().build_tree(0, 0, size - 1);

        for (int i = 0; i < 15; i++) {
            System.out.printf("tree[%d] : %d
", i, tree[i]);
        }
    }
}