网络最根本的作用是数据传输通信,与现实中的通信一样,网络通信也不得不面对安全性问
题,尤其是网络安全问题日益突出的今天。下面以两个端点为例介绍相关概念:
题,尤其是网络安全问题日益突出的今天。下面以两个端点为例介绍相关概念:
两个端点之间的安全通信具有哪些特性:
机密性:报文内容仅有发送方和接收方可以理解,使得即使窃听者获取了两端点间传输的报文,也无法获取报文的真正内容。
报文完整性:接收方接收的报文与发送方发送的报文内容一致,没有被恶意或意外篡改。
端点鉴别:发送方与接收方都可以证实在通信过程中,它们确实是自己所声称的身份。
运行安全性:在面对各个潜在的网络攻击时,系统具有预测、抵御这些攻击的能力。
如何使得两个端点间的通信满足上述特性?
在看到机密性时,最先被想到的应该是加密二字,我们通常将报文的最初形式称为明文,而
通过加密算法加密明文报文,生成的加密报文称为密文,该密文对于其他入侵者来说是无意
义的。在现代的众多密码系统中,加密技术本身是标准化的、公开发行的,任何人包括窃听
者在内都可以获取数据加密的方法。因此,我们需要一些秘密信息阻止窃听者解密数据,这
些秘密信息就是秘钥。
通过加密算法加密明文报文,生成的加密报文称为密文,该密文对于其他入侵者来说是无意
义的。在现代的众多密码系统中,加密技术本身是标准化的、公开发行的,任何人包括窃听
者在内都可以获取数据加密的方法。因此,我们需要一些秘密信息阻止窃听者解密数据,这
些秘密信息就是秘钥。
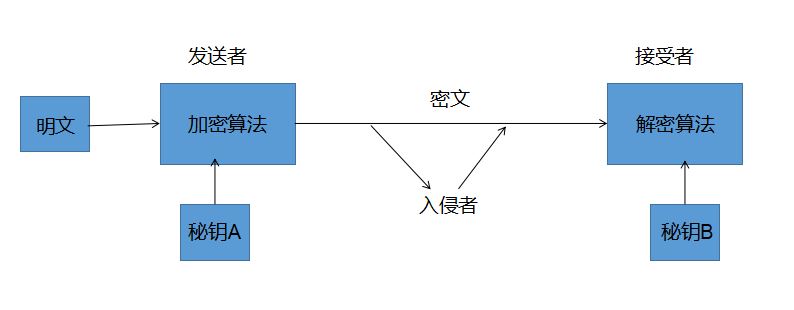
在上图中,发送方使用秘钥A 和明文作为加密算法的输入,生成的密文作为输出,接收方使
用秘钥B 和密文作为解密算法的输入,生成的明文作为输出。当秘钥A与秘钥B相同且都是秘
密的,称为对称秘钥系统;当秘钥A与秘钥B中一个是公开的,另一个是只有接收方或发送方
知道,称为公开秘钥系统。
用秘钥B 和密文作为解密算法的输入,生成的明文作为输出。当秘钥A与秘钥B相同且都是秘
密的,称为对称秘钥系统;当秘钥A与秘钥B中一个是公开的,另一个是只有接收方或发送方
知道,称为公开秘钥系统。
根据对称加密的工作方式,今天的对称加密技术可以分为两种宽泛的类型:流密码、块密码
块密码:
在块密码中将要加密的报文处理为k比特的块,每个块被独立加密。块密码采取一对一映射,将k比特块的明文映射为k比特的密文。块密码的每个块越大,则该密码就越安全。k 比特块
密码可能映射数量为 2^k。但对于较大的 k值,发送方与接收方之间就需要维护一张很大的
映射表,并且如果双方需要更改秘钥,就不得不重新生成该表,这几乎不能实现。因此,块
密码通常使用函数模拟随机排列表。
还存在一个问题,当传输长报文时,我们需要将报文切割成 k比特的块独立加密,但如果多
个明文块相同,那么它们的密文块也将相同,这将使得入侵者可能破解密文。为了解决这个
问题,我们在密文中加入某些随机性,使得相同明文块产生不同的密文。Linux 中密码存储
也采用了相同的思想,为了避免由于相同明文密码的密文形式相同而使得一些用户密码被猜
出,在计算用户密码的密文时会在明文秘密中加入随机值salt
个明文块相同,那么它们的密文块也将相同,这将使得入侵者可能破解密文。为了解决这个
问题,我们在密文中加入某些随机性,使得相同明文块产生不同的密文。Linux 中密码存储
也采用了相同的思想,为了避免由于相同明文密码的密文形式相同而使得一些用户密码被猜
出,在计算用户密码的密文时会在明文秘密中加入随机值salt
目前流行的块密码:DES(数据加密标准)、AES(高级加密标准)
根据入侵者所拥有的信息区分三种不同的入侵形式:
唯密文攻击:入侵者只能截取密文而不知道明文的内容已知明文攻击:入侵者知道部分明文与密文的匹配
选择明文攻击:入侵者能够选择某一明文并取得该明文的密文形式
对称加密要求发送方和接收方拥有相同的秘钥,但在网络中两个端点可能相隔千里,通信双
方能否在没有预先商定的共享秘钥的条件下进行加密通信呢?Diffie-Hellman秘钥交换解决
了这个问题,开创了如今的公开秘钥系统的发展之路。而公开秘钥系统的良好特性使得它不
仅可以用于加密,还可以用于鉴别和数字签名。
方能否在没有预先商定的共享秘钥的条件下进行加密通信呢?Diffie-Hellman秘钥交换解决
了这个问题,开创了如今的公开秘钥系统的发展之路。而公开秘钥系统的良好特性使得它不
仅可以用于加密,还可以用于鉴别和数字签名。

流行的公钥加密算法:Diffie-Hellman、RSA
公开秘钥密码的概念:
在发送方与接收方之间不存在共享秘钥的情况下,接收方具有两个秘钥,一个是众所周知的公钥,另一个是只有接收方知道的私钥。发送方可以使用接收方的公钥加密数据发送给接收
方,而此密文只能用接收方的私钥解密。同时使用接收方私钥加密的报文也可以用接收方的
公钥解密。
公开秘钥密码面对的问题:
由于接收方的公钥是众所周知的,除了发送方外其他入侵者也可以使用此公钥加密信息发送给接收方,那么应该如何鉴别发送方的身份呢?这就需要用数字签名将发送方和报文绑定。
密码散列函数:

密码散列函数通常用于提供报文完整性。散列函数给任意输入 X计算出一个称为散列的固定
长度的字符串 Y。任意两个不同的输入报文所得到的输出散列都不相同。即散列函数生成一
个属于数据的"指纹"(报文摘要)。
长度的字符串 Y。任意两个不同的输入报文所得到的输出散列都不相同。即散列函数生成一
个属于数据的"指纹"(报文摘要)。
著名的散列算法:MD5、SHA-1

在使用密码散列函数提供完整性时,接收方与发送方之间还需要一个鉴别秘钥,鉴别秘钥由
接收方与发送方共享,但对于其他人是秘密的。发送方在发送数据时,将报文m与鉴别秘钥k
一起作为密码散列函数的输入,而密码散列函数的输出称为报文鉴别码 MAC,发送方将报文
鉴别码M 加在报文上,生成扩展报文,并发送给接收方。接收方使用共享的鉴别秘钥与接收
的报文m 一起计算出报文鉴别码,并将其与接收到的报文鉴别码M 比较,如果两者相等,则
确定报文未被修改,且是由发送方发送的。
接收方与发送方共享,但对于其他人是秘密的。发送方在发送数据时,将报文m与鉴别秘钥k
一起作为密码散列函数的输入,而密码散列函数的输出称为报文鉴别码 MAC,发送方将报文
鉴别码M 加在报文上,生成扩展报文,并发送给接收方。接收方使用共享的鉴别秘钥与接收
的报文m 一起计算出报文鉴别码,并将其与接收到的报文鉴别码M 比较,如果两者相等,则
确定报文未被修改,且是由发送方发送的。
数字签名:

数字签名就是在数字领域实现证明身份的一种密码技术,数字签名可鉴别、不可伪造。因此
数字签名必须由某种与签名者相关且私密的东西生成。上述的私钥正好满足这点,当我们使
用发送方的私钥加密某个报文,如果接收方使用发送方的公钥解密后得到的明文与初始明文
相同则可以判断该报文是发送方发送的。因此,数字签名还可以提供完整性,使得接收方在
验证该报文未被篡改的同时验证该报文的源。
数字签名必须由某种与签名者相关且私密的东西生成。上述的私钥正好满足这点,当我们使
用发送方的私钥加密某个报文,如果接收方使用发送方的公钥解密后得到的明文与初始明文
相同则可以判断该报文是发送方发送的。因此,数字签名还可以提供完整性,使得接收方在
验证该报文未被篡改的同时验证该报文的源。
使用加密进行数据签名的缺点是加密、解密需要的开销过大,因此,更有效的方法是将散列
函数引入数字签名,发送方对报文的散列签名,而不是对报文本身签名。
函数引入数字签名,发送方对报文的散列签名,而不是对报文本身签名。
公钥认证:
数字签名的一个重要应用是公钥认证,即证实一个公钥属于某个特定的实体。将公钥与特定实体绑定通常是由认证中心CA完成的,CA的职责就是使识别和发行证书合法化。CA必须具有
一定公信力。
CA的作用:
1.CA证实一个实体的真实身份,这个实体可以是一个发送方、一台路由器等2.在CA验证了某实体的真实身份后,CA就会生成一个把其身份与实体公钥绑定起来的证书,
证书包含这个公钥和公钥所有者全局唯一的身份标识信息。
公钥认证的应用:IPsec、SSL
端点鉴别:
端点鉴别就是一个实体经过计算机网络向另一个实体证实其身份的过程。而网络中的端点鉴别是在报文和数据交换的基础上,作为鉴别协议ap的一部分独立完成。
ap1.0:发送方发送一个报文给接收方,声称它就是发送方。明显缺陷是,因为其他人也可以
向接收方发送报文说它是发送方。
向接收方发送报文说它是发送方。
ap2.0:当发送方有一个众所周知的IP地址时,接收方可以通过比较接收报文的源地址是否与
发送方众所周知的IP地址相同来鉴别。但这也不安全,因为我们知道可以在IP数据报中填入
我们希望的任意IP地址。
发送方众所周知的IP地址相同来鉴别。但这也不安全,因为我们知道可以在IP数据报中填入
我们希望的任意IP地址。
ap3.0:在发送方与接收方之间共享一个秘密口令,用于身份鉴别。看起来这种方式十分安全,
但它的缺陷是如果发送方端口被窃听,那么该口令就不在秘密。
但它的缺陷是如果发送方端口被窃听,那么该口令就不在秘密。
ap3.1:为了避免口令被入侵者获取,我们最先想到的应该是将口令加密,这样就可以防止入
侵者获取口令。但此时并不能解决鉴别问题,因为入侵者可以利用回放攻击,入侵者只需要
窃听发送方的通信,记录下该口令的加密版本,并向接收方发送该口令的加密版本,即可假
装它就是真正的发送者。
侵者获取口令。但此时并不能解决鉴别问题,因为入侵者可以利用回放攻击,入侵者只需要
窃听发送方的通信,记录下该口令的加密版本,并向接收方发送该口令的加密版本,即可假
装它就是真正的发送者。
ap4.0:不重数和对称秘钥机制的使用形成了ap4.0,ap3.1面对的问题是无法判断发送者的活
跃状态,在ap4.0中接收方发送给发送方一个不重数(在一个协议生存期中只使用一次的数),
发送方用它与接收方之间共享的对称秘钥来加密这个数,然后将加密的结果发送给接收方来
证明它的身份。
跃状态,在ap4.0中接收方发送给发送方一个不重数(在一个协议生存期中只使用一次的数),
发送方用它与接收方之间共享的对称秘钥来加密这个数,然后将加密的结果发送给接收方来
证明它的身份。
以上所述都站在满足两个端点之间的安全通信的部分特性的角度,下面将以安全电子邮件为
例,讲述如何利用上述方法满足两个端点之间的安全通信的全部特性:
例,讲述如何利用上述方法满足两个端点之间的安全通信的全部特性:
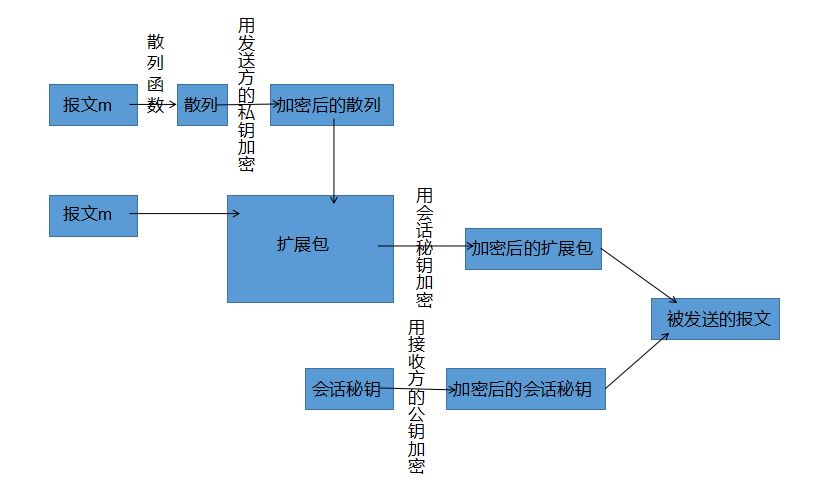
安全通信报文的生成过程:
1.计算将被发送报文的报文摘要,并使用发送方的私钥加密此摘要,将加密后的结果与初始报文作为一个新的报文。
2.随机选用一个会话秘钥加密这个新的报文,并将得到的结果与使用接收方公钥加密这个会
话秘钥所得的结果作为发送给接方的最终的报文。
为什么使用会话秘钥加密报文?
1.对称秘钥分发困难2.公开秘钥加密效率低下