要看懂本文可能至少需要知道什么是后缀(
还得知道一些自动机的概念(
和ac自动机有个很大的不同,sam它的字符是放在边上的(似乎放在点上也可以),因为大部分图都是这样的,(比如下图),把点看成了能接受从起点到该点的路径串的状态。
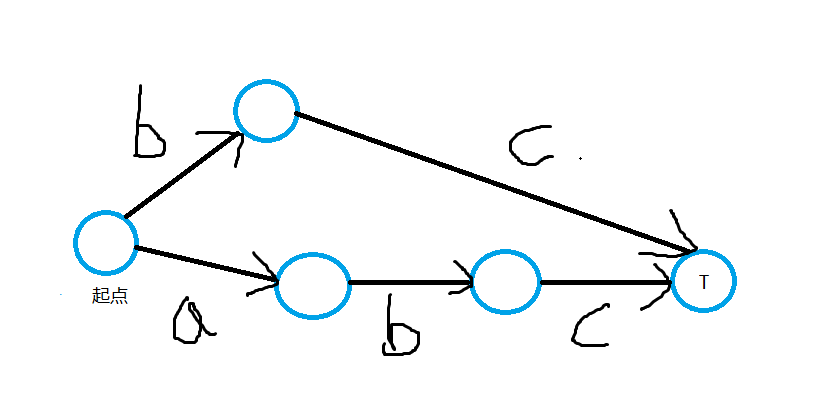
T状态能接受abc和bc字符串。 ( ps:图随手画的)
首先定义一些概念:
endpos(t):表示子串t的结束位置。比如aabaa,endpos(“aa”)={2,5}
在sam中,每个endpos(t)即为一个状态,也就是说几个endpos(t)相同的不同子串共用一个状态;显然abab中,ab和b是共用一个状态的。
先定义一个状态:x
string(x):表示x状态能接受的所有字符串。
可得性质1:
在string(x)中,短串是长串的后缀。
再定义几个东西:
string(x)_max,string(x)_min:分别其中的最长串、最短串。
又得性质2:
string(x)=={string(x)_min,string(x)_min+1,string(x)_min+2,,,,,,string(x)_max},就是说最长串的后缀连续出现在string(x)中,直到string(x)_min。
那么又会有疑问了,那长度小于string(x)_min的后缀呢?由于那些后缀的endpos(t)多了几个元素,便不和它们共用一个状态了。但还是有个东西把那些后缀也表示了出来。
定义Suffix指针:指向属于它后缀的状态。如下图绿色的线:
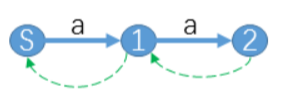
至此,,,似乎已经明白后缀自动机的结构了。
再补充两个点:
所有的子串即为从S出发的所有路径,即为所有状态的string(x)之和。
能轻易地知道每个子串的所有后缀。
状态总数为O(n)。
如何O(n)构造呢?
考虑递推,已经建好了前n-1个字符,再加入一个字符c,无非又多了n个子串。
定义pre[n-1]为前面n-1个字符构成的字符串。
这个时候我们只需看当时的末状态,即能接受pre[n-1]的那个状态,因为pre[n-1]的所有后缀加一个字符c就是新增的n-1个子串。
前面说过string(x)_max,string(x)_min,就不多说了,用一条边为c的边连接末状态和新状态,就解决了max-min+1个子串,也解决了pre[n]。
剩下可以分3类情况:
这个时候就需要借用末状态的Suffix指针了。
定义Suffix指针指向了y状态,上面说的新增状态为z。
1,y状态+c,在原有sam上不能发生转移,y新增一条边c指向z。
2,y状态+c,算了,太tm难了。