模拟赛 求和 题解

求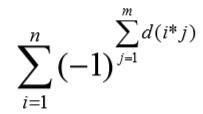

（d表示约数个数）
第一个sigma不能优化，需要优化第二个sigma（指数的那个）。
只有完全平方数的约数个数才是奇数，所以指数就相当于i×1,i×2……i×m中完全平方数的个数。
完全平方数中质因数分解后，所有指数都为偶数，所以对于每个i通过质因数分解可以得出至少乘多少才能成为一个完全平方数。
例如：(360=2^3×3^2×5^1,2和5的指数为奇数，所以360至少×10才能成为一个完全平方数。) （这个可以使用线性筛求得，设为(f(i))）
这样对于每个i计算m/f(i)，因为完全平方数×完全平方数之后还是完全平方数，所以再求得m/f(i)之内有几个完全平方数即可。而这个相当于(sqrt{m/f(i)})。
这样本题就在O(n)时间内得到解决。

线性筛代码：

	ch[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!sa[i])
		{
			ss[sl]=i;
			ch[i]=i;
			sl+=1;
		}
		for(int j=0;j<sl;j++)
		{
			if((ll)ss[j]*i>n)
				break;
			sa[ss[j]*i]=true;
			ch[ss[j]*i]=ch[i];
			if(ch[i]%ss[j]==0)
				ch[ss[j]*i]/=ss[j];
			else
				ch[ss[j]*i]*=ss[j];
			if(i%ss[j]==0)
				break;
		}
	}