核化主成分分析（Kernel PCA）应用及调参

核化这个概念在很多机器学习方法中都有应用，如SVM，PCA等。在此结合sklearn中的KPCA说说核函数具体怎么来用。

KPCA和PCA都是用来做无监督数据处理的，但是有一点不一样。PCA是降维，把m维的数据降至k维。KPCA恰恰相反，它是把m维的数据升至k维。但是他们共同的目标都是让数据在目标维度中（线性）可分，即PCA的最大可分性。

在sklearn中，kpca和pca的使用基本一致，接口都是一样的。kpca需要指定核函数，不然默认线性核。

首先我们用下面的代码生成一组数据。

import numpy as np
from sklearn.decomposition import PCA, KernelPCA
import matplotlib.pyplot as plt

import math
x=[]
y=[]
N = 500
for i in range(N):
    deg = np.random.randint(0,360)
    if np.random.randint(0,2)%2==0:
        x.append([6*math.sin(deg), 6*math.cos(deg)])
        y.append(1)
    else:
        x.append([15*math.sin(deg), 15*math.cos(deg)])
        y.append(0)
y = np.array(y)
x = np.array(x)
print('ok')

这些数据可以用下图来表示

显然，我们选的正样本（蓝）都落在一个半径为6的圆上，负样本（红）全选在一个半径为15的圆上。

这样的数据显然是线性不可分的。如果我们强行要用线性分类器来做，可以对原始数据做一个kpca处理。

如下代码：

kpca = KernelPCA(kernel="rbf", n_components=14)
x_kpca = kpca.fit_transform(x)

我们用rbf核，指定维度为14（为啥是14，后面说），也就是说吧X（2维）中的数据映射到14维的空间中去。

然后我们用一个线性的SVM分类器来对映射后的数据做一个分类，随机取80%做训练集，20%做测试集。

from sklearn import svm
clf = svm.SVC(kernel='linear')

clf.fit(x_kpca[:0.8*N],y[:0.8*N])
y0 = y[0.8*N:]
y1 = clf.predict(x_kpca[0.8*N:])
print(np.linalg.norm(y0-y1, 1))

此时，输出的是0，也就是说我们预测出的分类与正确的分类完全吻合，没有一个错误。此时分类器在这个数据集上是完全有效的。

综上所述，通过核化，可以把原本线性不可分的数据映射到高维空间后实现线性可分。

不过这个过程也不完全是那么简单，我们取不同的维度得到的结果可能相差甚远，也就是经典的调参问题。

在此，我测试了几组不同的k取值，得到不同k值条件下分类准确率值。如下图。

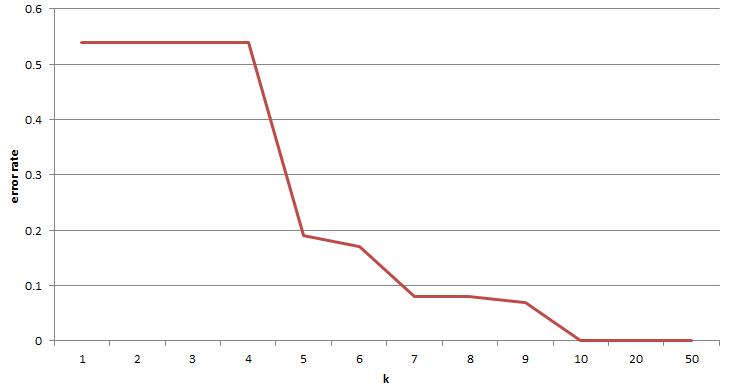
可以看出，不同的k值对结果是有影响的。但不同的数据集可能不一样，所以需要进行调参。我这个取14就全ok了。