CF600D 题解
题目的字面意思
给出一个无向图,要求这个图是和谐的,和谐的定义是,如果A 到 C(A < B < C)有一条路, 那么 B 到C也有一条路。数据范围给的是2e5
然后我们可以意识到,如果一个子集中的所有元素都是连续的,那么这个子集,就是和谐的,因为联通图,任意两点都可以到达。如果说一个子集的元素不是连续的话,那么就一定需要有一条或者多条路径连到别的子集里去。给出两个例子说明:
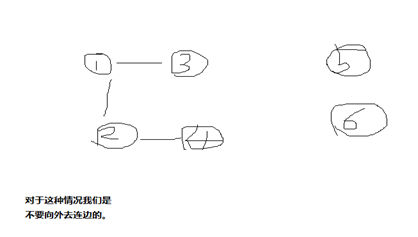
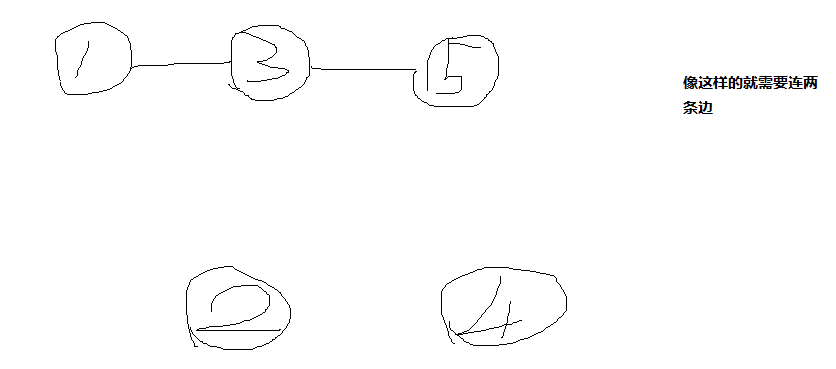
然后就变成了怎么处理的问题。
我使用了并查集,对于相连的点,都合并到小的那个点去,然后更新size数组和maxx数组(size[i]用来记录此时集合i的个数, maxx用来记录集合中的最大值)
然后我们就可以很愉快的判断,如果maxx[i] – i + 1 == size[i], 那么说明这个集合是和谐的,也就是不需要向外面连边的。
那么对于不满足条件的一个怎么处理呢?
很简单遍历i+1到maxx[i], 对需要合并进来的集合进行合并就可以,在这个过程中, maxx[i]是一直在更新的, 所以这个思想的复杂度是O(n), 就很优雅。
最后放上菜鸟代码
1 #include <stdio.h> 2 #include <algorithm> 3 using namespace std; 4 const int N = 2e5+10; 5 int fa[N], maxx[N], size[N]; 6 int find(int x) //并查集基本操作 7 { 8 if(x==fa[x]) return x; 9 return fa[x] = find(fa[x]); 10 } 11 int main() 12 { 13 int x, y, fx, fy; 14 int n, m, res = 0; 15 scanf("%d %d", &n, &m); 16 for(int i = 1; i <= n; i++) //并查集的初始化 17 { 18 fa[i] = i; 19 maxx[i] = i; 20 size[i] = 1; 21 } 22 for(int i = 1; i <= m; i++) 23 { 24 scanf("%d %d", &x, &y); 25 //判断 然后建里并查集 26 fx = find(x); fy = find(y); 27 if(fx < fy) 28 { 29 fa[fy] = fx; 30 size[fx] += size[fy]; 31 maxx[fx] = max(maxx[fx], maxx[fy]); 32 }else if(fy < fx){ 33 fa[fx] = fy; 34 size[fy] += size[fx]; 35 maxx[fy] = max(maxx[fx], maxx[fy]); 36 } 37 } 38 for(int i = 1; i <= n; ) 39 { 40 if(fa[i]==i) //这个判断没有应该是可以的 41 { 42 //满足条件 43 if(size[i]==maxx[i]-i+1) i += size[i]; 44 else{ 45 // 不满足条件 46 for(int j = i+1; j <= maxx[i]; j++) 47 { 48 //动态更新 答案++ 49 if(find(j)!=i) 50 { 51 fa[j] = i; 52 size[i] += size[j]; 53 maxx[i] = max(maxx[i], maxx[j]); 54 res++; 55 } 56 } 57 } 58 } 59 } 60 printf("%d\n", res); 61 62 }