想必大家都可以非常迅速的解出一个二元一次方程组,
那么三元呢(这也还好),那么再多一些未知数?
于是这里就要介绍到高斯消元的方法了...
本人蒟蒻到现在才学高斯消元,请不要介意方法过于垃圾
--------------------------------------------------------------------------------------------------
首先假设你拿到了一个n元方程组,那么它应该有n个方程,每个方程有n+1个系数,
好于是我们把他们全部弄到一个n*(n+1)的矩阵中,这里简称为系数矩阵
第一步:我们先把每一行的系数都除以这一行的第一个数

第二步:从第一行到第n行分别控制x1...xn的解,因此你需要把第i行的第i列的系数化为1以此来求解方程,
第三步:在处理第i行的时候,把第i+1行到第n行的数通过加减消元法处理
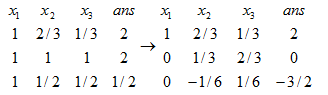
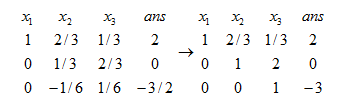
第四步:那么求出这个答案就是最后的答案数组了,
求答案是xn的值是a[n][n+1],然后如果求x(n-1)的值就是将xn的值代入a[n-1][n],然后求出x(n-1)的值
于是乎 x1=-1,x2=3,x3=-6
以上就是关于高斯消元简要的介绍.
下面是两种不同题目下的高斯消元
(1) 方程保证是整数解,且系数大小均为long long 以内
注意:此处运用到简单的高精度,以及取模

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 #include<algorithm> 6 #define ll long long 7 using namespace std; 8 const ll p=1000000000000000009; 9 ll a[210][210],ans[210]; 10 ll mul(ll a,ll b){return (__int128)a*b%p;} 11 ll inv(ll a){ 12 ll res=1,b=p-2; 13 while (b){ 14 if (b&1) res=mul(res,a); b>>=1; a=mul(a,a); 15 } return res; 16 } 17 ll Div(ll a,ll b){return mul(a,inv(b));} 18 ll read(){ 19 char ch[1010]; scanf("%s",ch+1); 20 ll res=0,len=strlen(ch+1); 21 for (int i=1;i<=len;++i){ 22 res=mul(res,10)+ch[i]-'0'; 23 if (res>p) res-=p; 24 } 25 return res; 26 } 27 28 29 int main() { 30 int n;scanf("%d",&n); 31 for(int i=1;i<=n;i++){ 32 for(int j=1;j<=n;j++) 33 scanf("%lld",&a[i][j]); 34 a[i][n+1]=read(); 35 ll res=a[i][1]; 36 for(int j=1;j<=n+1;j++) a[i][j]=Div(a[i][j],res); 37 } 38 for(int i=1;i<=n;i++){ 39 if (a[i][i]==0) {puts("zzylihai"); return 0;} 40 for(int j=i+1;j<=n+1;++j) 41 a[i][j]=Div(a[i][j],a[i][i]); 42 a[i][i]=1; 43 for(int j=i+1;j<=n;j++) { 44 for(int k=i+1;k<=n+1;k++){ 45 a[j][k]-=mul(a[j][i],a[i][k]); 46 if (a[j][k]<0) a[j][k]+=p; 47 } 48 a[j][i]=0; 49 } 50 } 51 for(int i=n;i>=1;i--) { 52 ll res=a[i][n+1]; 53 for(int j=i+1;j<=n;j++) { 54 res-=mul(ans[j],a[i][j]); 55 if (res<0) res+=p; 56 } 57 ans[i]=Div(res,a[i][i]); 58 } 59 for(int i=1;i<=n;i++) printf("%lld ",ans[i]); 60 return 0; 61 }
(2)方程为实数解,要判断是否无解

#include<iostream> #include<cstring> #include<cstdio> #include<cmath> #include<algorithm> using namespace std; double a[210][210],ans[210]; int n; int main() { scanf("%d",&n); for(int i=1;i<=n;i++){ for(int j=1;j<=n+1;j++) scanf("%lf",&a[i][j]),a[i][j]*=1.00; double res=a[i][1]; for(int j=1;j<=n+1;j++) a[i][j]=(double)a[i][j]/res; } for(int i=1;i<=n;i++){ if (a[i][i]==0) {puts("No solution"); return 0;} for(int j=i+1;j<=n+1;++j) a[i][j]/=a[i][i]; a[i][i]=1; for(int j=i+1;j<=n;j++) { for(int k=i+1;k<=n+1;k++) a[j][k]-=a[j][i]*a[i][k]; a[j][i]=0; } } for(int i=n;i>=1;i--) { double res=a[i][n+1]; for(int j=i+1;j<=n;j++) res-=ans[j]*a[i][j]; ans[i]=res/a[i][i]; } for(int i=1;i<=n;i++) printf("%.0lf ",ans[i]); return 0; }
