数组中的逆序对

题目描述

　　在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

输入描述:

　　题目保证输入的数组中没有的相同的数字

　　数据范围：

　　对于%50的数据,size<=10^4

　　对于%75的数据,size<=10^5

　　对于%100的数据,size<=2*10^5

示例1

输入

  1,2,3,4,5,6,7,0

输出

  7



提交链接：点击




思路：利用归并排序的方法。

　　

　　我们以数组｛7, 5, 6, 4｝为例来分析统计逆序对的过程。每次扫描到一个数字的时候，我们不能拿它和后面的每一个数字作比较，否则时间复杂度就是O(n^5)，因此我们可以考虑先比较两个相邻的数字。

 　　

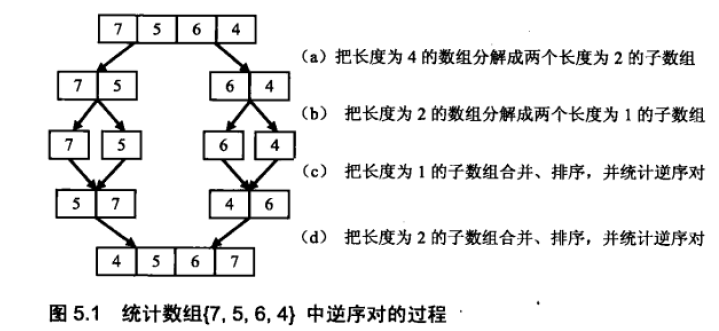
　　如图5 . 1 ( a )和图5.1 ( b）所示，我们先把数组分解成两个长度为2的子数组， 再把这两个子数组分别拆分成两个长度为1 的子数组。接下来一边合并相邻的子数组， 一边统计逆序对的数目。在第一对长度为1 的子数组｛7｝、｛5｝中7 大于5 ， 因此（7, 5）组成一个逆序对。同样在第二对长度为1 的子数组｛6｝、｛4｝中也有逆序对（6, 4）。由于我们已经统计了这两对子数组内部的逆序对，因此需要把这两对子数组排序（ 图5.1 ( c）所示），以免在以后的统计过程中再重复统计。

 

注　图中省略了最后一步， 即复制第二个子数组最后剩余的4 到辅助数组中. 
(a) P1指向的数字大于P2指向的数字，表明数组中存在逆序对．P2 指向的数字是第二个子数组的第二个数字， 因此第二个子数组中有两个数字比7 小． 把逆序对数目加2，并把7 复制到辅助数组，向前移动P1和P3. 
(b) P1指向的数字小子P2 指向的数字，没有逆序对．把P2 指向的数字复制到辅助数组，并向前移动P2 和P3 . 
(c) P1指向的数字大于P2 指向的数字，因此存在逆序对． 由于P2 指向的数字是第二个子数组的第一个数字，子数组中只有一个数字比5 小． 把逆序对数目加1 ，并把5复制到辅助数组，向前移动P1和P3 .

　　接下来我们统计两个长度为2 的子数组之间的逆序对。我们在图5.2 中细分图5.1 ( d）的合并子数组及统计逆序对的过程。
　　我们先用两个指针分别指向两个子数组的末尾，并每次比较两个指针指向的数字。如果第一个子数组中的数字大于第二个子数组中的数字，则构成逆序对，并且逆序对的数目等于第二个子数组中剩余数字的个数（如图5.2 (a)和图5.2 (c)所示）。如果第一个数组中的数字小于或等于第二个数组中的数字，则不构成逆序对（如图5.2 (b)所示〉。每一次比较的时候，我们都把较大的数字从·后往前复制到一个辅助数组中去，确保辅助数组中的数字是递增排序的。在把较大的数字复制到辅助数组之后，把对应的指针向前移动一位，接下来进行下一轮比较。
　　经过前面详细的诗论， 我们可以总结出统计逆序对的过程：先把数组分隔成子数组， 先统计出子数组内部的逆序对的数目，然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中，还需要对数组进行排序。如果对排序贺，法很熟悉，我们不难发现这个排序的过程实际上就是归并排序。
---------------------
原文：https://blog.csdn.net/derrantcm/article/details/46761051

代码：

class Solution {
public:
    int InversePairs(vector<int> data) {
        //归并   找逆序对
        if(data.size()<=0) return 0;
        int low=0,high=data.size()-1;
        vector<int> temp;
        for(int i=0;i<data.size();i++)
           temp.push_back(data[i]);
        long long result=InverseP(data,temp,low,high);
        return result%1000000007;

    }
    long long InverseP(vector<int> &data,vector<int> &temp, int low, int high){
        if(low==high){
            temp[low]=data[low];
            return 0;
        }
        int mid=(low+high)/2;
        long long left=InverseP(data,temp,low,mid);  //找到左部分的逆序对
        long long right=InverseP(data,temp,mid+1,high); //找到右部分的逆序对
        int currIndex=high;
        //计算左右的逆序对
        long long count=0;
        int i=mid;      //左部分尾指针
        int j=high;     //右部分尾指针
        while(i>=low && j>=mid+1){
            if(data[i]>data[j]){
                count+=(j-mid)%1000000007;
                temp[currIndex--]=data[i--];
            }else{
                temp[currIndex--]=data[j--];
            }
        }
        while(i>=low){
            temp[currIndex--]=data[i--];
        }
        while(j>=mid+1){
            temp[currIndex--]=data[j--];
        }
        //将temp已排序好的数字赋值到data
        currIndex=low;
           while(low<=high){
            data[low++]=temp[currIndex++];
        }
        return left+right+count;
    }
};